Projet 1 : Modélisation du robot « Axis »

On étudie le robot « Axis » cf. Fig. 93. Il s’agit d’un robot composé de 5 bras identiques possédant chacun 3 articulations. La vidéo suivante montre le fonctionnement du système : lien YouTube

Fig. 93 Photo du robot Axis

L’objectif du projet est d’établir des lois de commandes au niveau des moteurs (servomoteurs) afin d’effectuer une trajectoire spécifique au niveau des 5 effecteurs. Ce projet est scindé en 2 parties. La première partie consiste à écrire les modèles géométriques et cinématiques directs et inverses. La seconde partie est dédiée à la mise en place des lois de commande des actionneurs (positions et vitesses en fonction du temps) afin que les effecteurs puissent manipuler une sphère ou un plateau.

Afin de résoudre le problème, il est préférable de tout paramétrer par des variables pour établir une solution la plus générale possible. Le sujet est très ouvert. Libre à vous de le mener de la manière dont vous le souhaitez, d’aller plus loin dans les développements . Les questions sont présentes uniquement pour vous guider.

Si une solution est aboutie d’un point de vue logiciel, très propre, et est bien documentée il est envisageable d’acheter quelques servomoteurs et de réaliser une maquette d’un bras, voire du système entier. Pour informations les servomoteurs utilisés dans la vidéo coûtent 500 euros / pièce. Et à raison de 3 servomoteurs par bras et de 5 bras, cela fait cher !

Mise en place des modèles géométriques et cinématiques directs et inverses

Le schéma cinématique d’un des 5 bras du robot est proposé en annexe. On considérera pour simplifier le travail que les 5 bras sont équirépartis angulairement sur le socle. On nommera effecteur le point physique \(P_i\) situé à la terminaison du bras \(i\).

On utilisera les notations \(\beta_i, a_i, b_i, ...\) pour décrire les paramètres géométriques et \(\theta_{1i}, \theta_{2i}, \theta_{3i}\) pour décrire les paramètres articulaires.

Question 1.1 : Établir le paramétrage d’un bras \(i\) au sens de Denavit Hartenberg.

Question 1.2 : Établir le modèle géométrique direct en position de l’effecteur \(i\) dans le repère \(\mathcal{R}_0\).

Question 1.3 : Établir le modèle géométrique inverse en position de l’effecteur.

Question 1.4 : Établir les modèles cinématiques direct et inverse.

Mise en place des lois de commande

Question 2.1 : Établir les lois de commande des actionneurs d’un bras afin que le mouvement de l’effecteur décrive un arc de cercle d’un diamètre \(d\) de centre \(P = (x_p,y_p,z_p)\) et cela à vitesse \(V_{eff}\) constante.

Pour avoir une solution fonctionnelle, il peut-être intéressant d’ajouter une phase permettant à l’effecteur de revenir à sa position afin d’effectuer un cycle.

Question 2.1 : En déduire les lois de commande des 12 autres actionneurs associés aux 4 bras restants.

Annexes

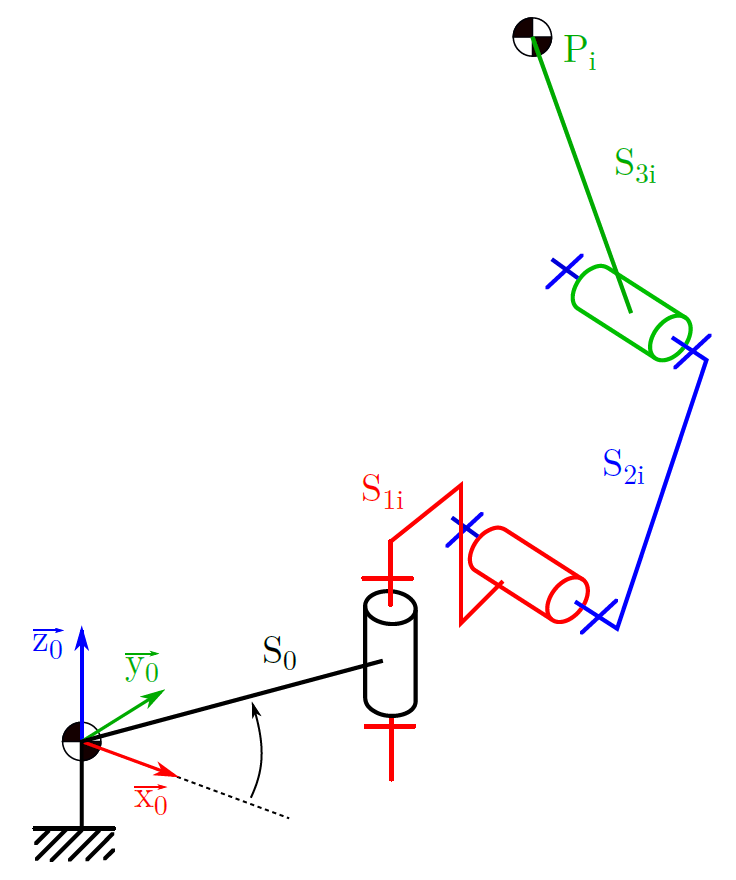
Fig. 94 Schéma cinématique d’un bras « i »