Modélisation géométrique

Modèles géométriques et structures mécaniques

Structures mécaniques

Les structures mécaniques peuvent être classées en quatre catégories principales (Fig. 12) :

• les structures simples ouvertes : il existe une chaîne cinématique ouverte ;

• les structures simples fermées : il existe une chaîne cinématique fermée ;

• les structures parallèles : il existe au moins deux chaînes cinématiques fermées ;

• les structures hybrides (ouvertes) : c’est une composition des catégories précédentes.

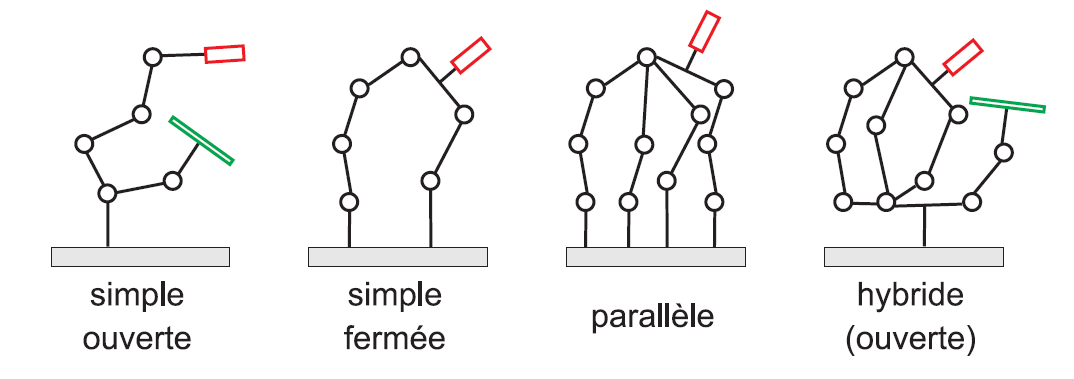
Fig. 12 Classification des structures mécaniques

Paramétrage des structures ouvertes simples

Convention de Denavit et Hartenberg modifiée

Soient deux solides \(\S_{i-1}\) et \(S_i\) en liaison. On définit le positionnement du repère \(\mathcal{R}_i\) associé au solide \(S_i\) à partir du repère \(\mathcal{R}_{i-1}\) :

• \(\overrightarrow{z_i}\) vecteur unitaire selon l’axe caractéristique de la liaison entre \(S_{i-1}\) et \(S_i\)

• \(\overrightarrow{x_i}\) vecteur unitaire selon la normale commune aux deux liaisons \(\overrightarrow{z_{i}}\) et \(\overrightarrow{z_{i+1}}\)

  • si les deux axes \(\overrightarrow{z_{i}}\), \(\overrightarrow{z_{i+1}}\) sont parallèles, la normale commune est choisie arbitrairement pour simplifier le paramétrage

  • si les deux axes \(\overrightarrow{z_{i}}\), \(\overrightarrow{z_{i+1}}\) sont confondus, l’orientation de \(\overrightarrow{x_{i}}\) doit être choisie suivant des considérations de simplification

• \(y_{i}\) est défini tel que la base \((\overrightarrow{x_{i}}, \overrightarrow{y_{i}}, \overrightarrow{z_{i}})\) soit orthonormée directe

• \(O_i\) est le centre associée à la base \((\overrightarrow{x_{i}}, \overrightarrow{y_{i}}, \overrightarrow{z_{i}})\) pour former le repère \(\mathcal{R}_i\) attaché au corps \(S_i\). \(O_i\) est défini par l’intersection de \(\overrightarrow{z_i}\) avec \(\overrightarrow{x_i}\).

Le passage entre les repères \(\mathcal{R}_{i-1}\) et \(\mathcal{R}_i\) est donné par les 4 paramètres suivants :

• \(d_i\) : distance entre les axes \(\overrightarrow{z_{i-1}}\) et \(\overrightarrow{z_{i}}\), mesurée le long de l’axe \(\overrightarrow{x_{i-1}}\)

• \(\alpha_i\) : angles entre les axes \(\overrightarrow{z_{i-1}}\) et \(\overrightarrow{z_{i}}\), mesurée autour de l’axe \(\overrightarrow{x_{i-1}}\)

• \(r_i\) : distance entre les axes \(\overrightarrow{x_{i-1}}\) et \(\overrightarrow{x_{i}}\), mesurée le long de l’axe \(\overrightarrow{z_{i}}\)

• \(\theta_i\) : angle entre les axes \(\overrightarrow{x_{i-1}}\) et \(\overrightarrow{x_{i}}\), mesurée autour de l’axe \(\overrightarrow{z_i}\)

Fig. 13 Paramétrisation selon la convention de DH modifiée

Le passage du repère \(\mathcal{R}_{i-1}\) au repère \(\mathcal{R}_{i}\) fait apparaître 4 transformations :

• une translation \(d_i\) selon \(\overrightarrow{x_{i-1}}\)

• une rotation \(\alpha_i\) selon \(\overrightarrow{x_{i-1}}\)

• une translation \(r_i\) selon \(\overrightarrow{z_{i}}\)

• une rotation \(\theta_i\) selon \(\overrightarrow{z_{i}}\)

En regroupant les transformations effectuées selon les axes \(\overrightarrow{x_{i-1}}\) et \(\overrightarrow{z_{i}}\), il est possible de faire le changement de repère entre \(\mathcal{R}_{i-1}\) et \(\mathcal{R}_{i}\) en associant deux opérateurs homogènes \(\mathbf{T}_{i-1\, int}\) et \(\mathbf{T}_{int\, i}\) qui font transiter par un repère intermédiaire \(\mathcal{R}_{int}\) :

\[\begin{split} \begin{align*} \mathcal{R}_{i-1} \longrightarrow \mathcal{R}_{int} & \qquad \qquad \text{puis} & \mathcal{R}_{int} \longrightarrow \mathcal{R}_{i} \\ \mathbf{T}_{i-1\, int}(d_i, \alpha_i) & & \mathbf{T}_{int \, i}(r_i, \theta_i) \end{align*} \end{split}\]

avec :

\[\begin{split} \begin{equation} \mathbf{T}_{i-1\, int} = \begin{bmatrix} 1 & 0 & 0 & d_i \\ 0 & \text{C}\alpha_i & -\text{S}\alpha_i & 0 \\ 0 & \text{S}\alpha_i & \text{C}\alpha_i & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \qquad \mathbf{T}_{int\, i} = \begin{bmatrix} \text{C}\theta_i & -\text{S}\theta_i & 0 & 0 \\ \text{S}\theta_i & \text{C}\theta_i & 0 & 0 \\ 0 & 0 & 1 & r_i \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation} \end{split}\]

Il est alors possible d’exprimer pour chaque liaison un opérateur homogène correspondant :

\[\begin{split} \begin{equation} \mathbf{T}_{(i-1) i} = \mathbf{T}_{i-1\, int} \mathbf{T}_{int\, i} = \begin{bmatrix} \text{C}\theta_i & -\text{S}\theta_i & 0 & d_i \\ \text{C}\alpha_i\text{S}\theta_i & \text{C}\alpha_i\text{C}\theta_i & -\text{S}\alpha_i & -r_i \text{S}\alpha_i \\ \text{S}\alpha_i\text{S}\theta_i & \text{S}\alpha_i\text{C}\theta_i & \text{C}\alpha_i & r_i \text{C}\alpha_i \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation} \end{split}\]

Les valeurs des paramètres, constantes géométriques ou variables selon la nature de la liaison, sont souvent formalisées dans un tableau de la forme :

	\(d_i\)	\(\alpha_i\)	\(r_i\)	\(\theta_i\)
\(\mathbf{T}_{01}\)
\(\mathbf{T}_{12}\)
\(\cdots\)

L’expression d’un point \(P\) appartenant au solide \(n\) (repère \(\mathcal{R}_n\)), peut donc se faire dans le Repère \(\mathcal{R}_0\) (bâti par exemple) par :

\[ \begin{equation} ^0\mathbf{P} = \mathbf{T}_{01}\ \mathbf{T}_{12} \cdots \mathbf{T}_{(n-1)n}\ ^n\mathbf{P} \end{equation} \]

Dans le cas d’une architecture sérielle où \(\mathcal{R}_0\) est le repère lié à la pièce et \(\mathcal{R}_n\) celui lié à l’effecteur, nous obtenons ainsi une fonction faisant le lien entre l’extrémité et la base du système sous forme de coordonnées homogènes :

\[ \begin{equation} ^0\mathbf{P} = \mathbf{T}_{0n}\ ^n\mathbf{P} \quad \text{où} \quad \mathbf{T}_{0n} = \text{fct}(d_i, \alpha_i, r_i, \theta_i) \quad i \in \left[1 \cdots n\right] \end{equation} \]

On remarque que dans cette écriture ne sont pas différentiées les variables articulaires des paramètres géométriques. Cette différence est faite lors de l’écriture de chaque type de liaison.

Paramétrage des structures fermées

Problématique

Il existe, suivant les structures de machines, plusieurs solutions pour décrire la transformation géométrique directe. Par exemple, pour la plateforme de Gough-Stewart, il en existe quatre, c’est-à-dire qu’à une configuration correspond quatre positionnements différents de l’effecteur. Une approche numérique est nécessaire pour déterminer de proche en proche la solution souhaitée.

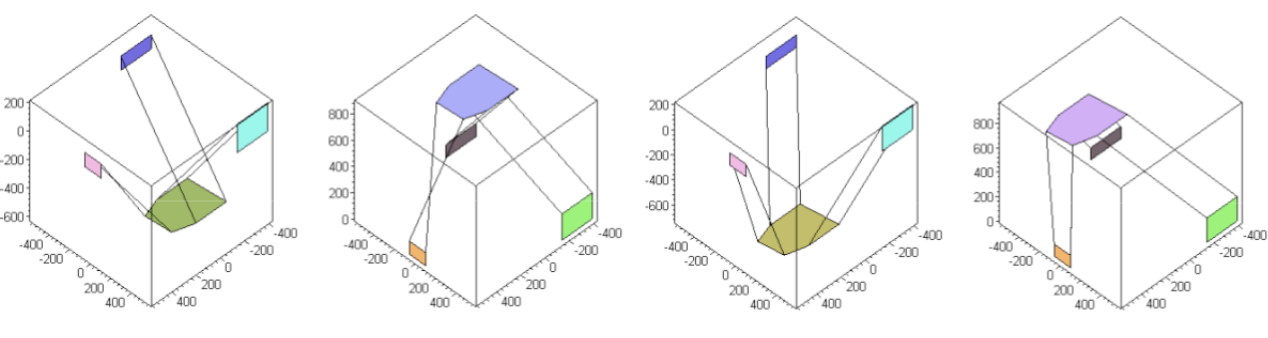
Fig. 14 Illustration des 4 solutions existantes pour une même configuration

Les difficultés de modélisation sont inversées par rapport aux structures sérielles : il est plus aisé de déterminer les valeurs des paramètres articulaires pour respecter un positionnement de l’effecteur que de déterminer le positionnement de l’effecteur pour une configuration articulaire donnée. Dans la suite du document, la méthode de Merlet, méthode spécifique aux architectures parallèles, est présentée. Elle permet une démarche systématique pour paramétrer et poser le problème.

Modélisation géométrique : Méthode de Merlet

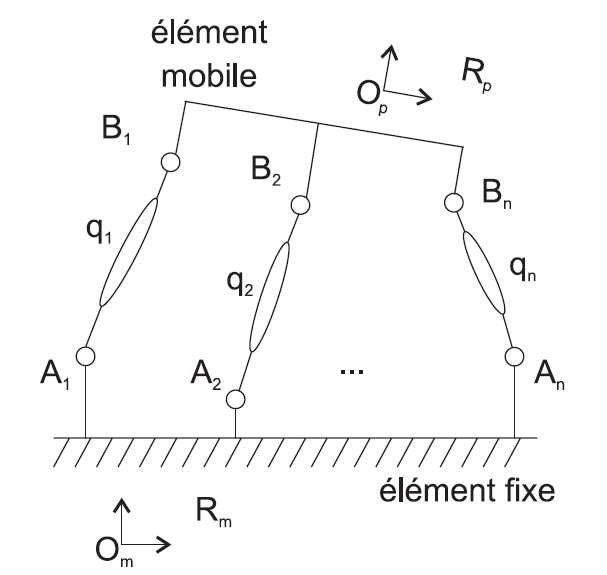
Fig. 15 Paramétrisation de la structure mécanique

• soit un élément fixe, lié au repère \(\mathcal{R}_m = (O_m,\overrightarrow{x_m},\overrightarrow{y_m},\overrightarrow{z_m})\)

• soit un élément mobile, lié au repère \(\mathcal{R}_p = (O_p,\overrightarrow{x_p},\overrightarrow{y_p},\overrightarrow{z_p})\)

• soit \(A_i\, , i = 1 \cdots n\), les liaisons liées à l’élément fixe. La position et la géométrie de ces liaisons sont supposées fixes et connues (valeurs nominales ou identifiées). Les vecteurs \(\overrightarrow{O_m A_i}\) sont donc des paramètres géométriques du mécanisme notés plus globalement \(\xi\).

• soit \(B_i\, , i = 1 \cdots n\), les liaisons liées à l’élément mobile. De même, la géométrie \(\overrightarrow{O_p B_i}\) est fixe et connue et fait partie des paramètres géométriques \(\xi\).

• chaque vecteur \(\overrightarrow{A_i B_i}\) est noté « jambe », ce sont les liaisons motorisées de la structure ; les variables de commande dites articulaires sont notées \(q_i\).

• soit \(\overrightarrow{X}\) le positionnement de l’effecteur de la plateforme mobile dans \(\mathcal{R}_m\)

Relations géométriques

L’écriture se fait par fermeture géométrique pour chaque jambe :

\[ \begin{equation} \overrightarrow{A_i B_i} = \overrightarrow{A_i O_m} + \overrightarrow{O_m O_p} + \overrightarrow{O_p B_i} \end{equation} \]

où chaque terme s’exprime en fonction de :

• \(\overrightarrow{A_i B_i}\) : \(\xi\) (constantes géométriques pour chaque jambe) et \(q_i\) (variables articulaires)

• \(\overrightarrow{A_i O_m}\) : \(\xi\) (constantes géométriques dans \(\mathcal{R}_m\))

• \(\overrightarrow{O_m O_p}\) : \(\overrightarrow{X}\)

• \(\overrightarrow{O_p B_i}\) : \(\xi\) (constantes géométriques dans \(\mathcal{R}_p\))

ce qui permet d’arriver à une forme générale séparant dans chacun des membres les paramètres articulaires des paramètres de positionnement :

\[ \begin{equation} \overrightarrow{H}_2(q_i,\xi) = \overrightarrow{H}_2(X,\xi) \end{equation} \]

Matrice de transformation homogène

Dans le cas des structures parallèles, il existe une seule transformation \(\mathbf{T}_{mp}\) permettant d’exprimer directement le positionnement du repère associé à la plateforme mobile \(\mathcal{R}_p\) par rapport au repère associé à la base fixe \(\mathcal{R}_m\). L’expression du positionnement de l’effecteur \(^m\mathbf{P}_{eff}\) exprimé dans le repère \(\mathcal{R}_m\) s’exprime en fonction de son expression dans \(\mathcal{R}_p\), \(^p\mathbf{P}_{eff}\) par la relation :

(9)\[ \begin{equation} ^m\mathbf{P}_{eff} = \mathbf{T}_{mp} \ ^p\mathbf{P}_{eff} \end{equation} \]