Ctrl+K

TD n°3 : Modélisations cinématiques - Singularités

TD n°3 : Modélisations cinématiques - Singularités#

On étudie le robot Scara 4 axes, référencé « s600 » de marque Adept donné en Fig. 39 :

../_images/photo_SCARA1.png

Fig. 39 Robot SCARA s600#

Pour cette étude, on tiendra pas compte des courses de chaque axe afin de ne pas être limité dans les mouvements ; on négligera de même les potentielles collisions.

Modélisations cinématiques#

Calcul analytique#

Question 1.1 : A partir du schéma cinématique et du paramétrage DHm effectué au TD n°1, déterminer les expressions des vecteur rotation et vecteur vitesse du référentiel associé à l’effecteur \(\mathcal{R}_{\text{eff.}}\) dans son mouvement par rapport au référentiel de base \(\mathcal{R}_0\).

On utilisera préférentiellement la composition du mouvement et la relation de changement de point pour le calcul du vecteur vitesse.

Question 1.2 : En déduire l’expression de la matrice jacobienne \(\mathbf{J}\) et donc le Modèle Cinématique Direct (MCD).

Différentiation - dérivation#

Question 1.3 : Retrouver rapidement le résultat précédent par dérivation du Modèle Géométrique Direct établi au TD n°1.

Jacobien de base#

Question 1.4 : Déterminer le jacobien de base \(\mathbf{J}_n\) à partir des contributions de chaque liaison \(\mathbf{J}_{n,k}\).

On se donne maintenant comme variables de l’espace des tâches les composantes dans un système de coordonnées cylindriques (au lieu du système cartésien classique).

Question 1.5 : Déterminer l’expression de la matrice \(\mathbf{\Omega}\), lien entre le jacobien de base \(\mathbf{J}_n\) et les variables de l’espace des tâches pour la cinématique \(\dot{\mathbf{X}}\).

Recherche des singularités#

Question 2.1 : A partir de l’étude de la jacobienne \(\mathbf{J}\), déterminer les singularités pour ce robot.

Question 2.2 : Représenter sur un schéma cinématique les différents cas rencontrés ; Expliquer les singularités.

Question 2.3 : Représenter les branches de singularités dans l’espace des tâches et dans l’espace articulaire.

Synthèse#

Analyser le modèle du robot implémenté dans l’application « RoboDK ». Pour cela,

  • modifier le paramétrage du robot pour éviter tout problème lié aux courses ;

  • positionner le robot dans sa configuration singulière « repliée » ;

  • solliciter le robot par des translations « tangentes au rayon » (attention au pas de calcul).

Annexes#

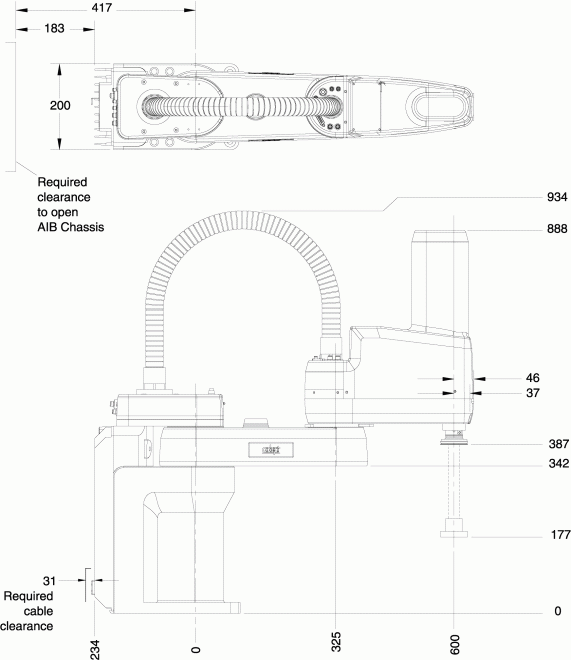
../_images/vue_cote.png

Fig. 40 Caractéristiques dimensionnelles#

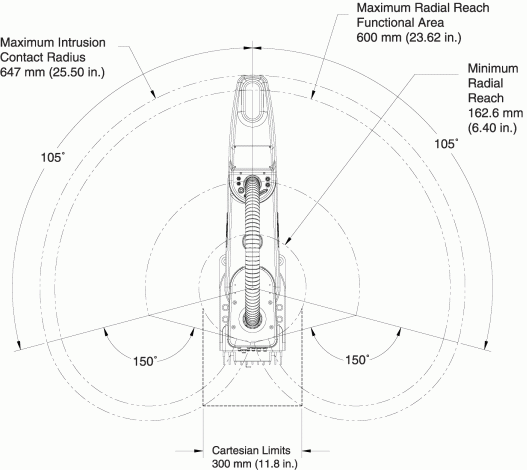
../_images/volume.png

Fig. 41 Surface balayée par l’effecteur#

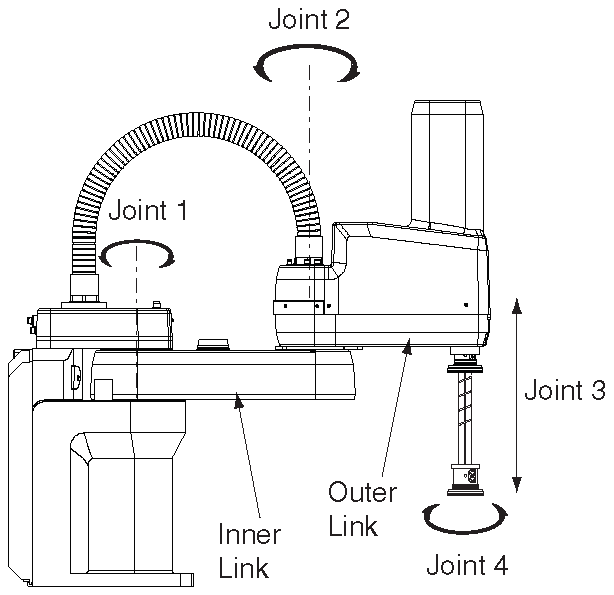
../_images/cinematique.png

Fig. 42 Extrait de documentation : cinématique#

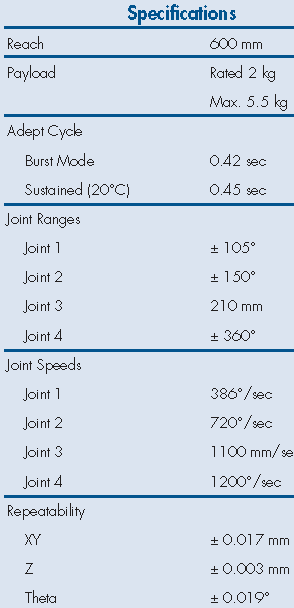
../_images/specifications.png

Fig. 43 Extrait de documentation : spécifications#

Contenu