TD n°4 : Modes d’interpolation des trajets#
On étudie le centre d’usinage 4 axes Realméca de l’atelier de fabrication du DGM. C’est un centre d’usinage à broche horizontale possédant 3 axes de translation de variables \(X_m\), \(Y_m\), \(Z_m\) ainsi qu’un axe de rotation au niveau du plateau de variable \(B\). La modélisation cinématique est donnée en Fig. 49.
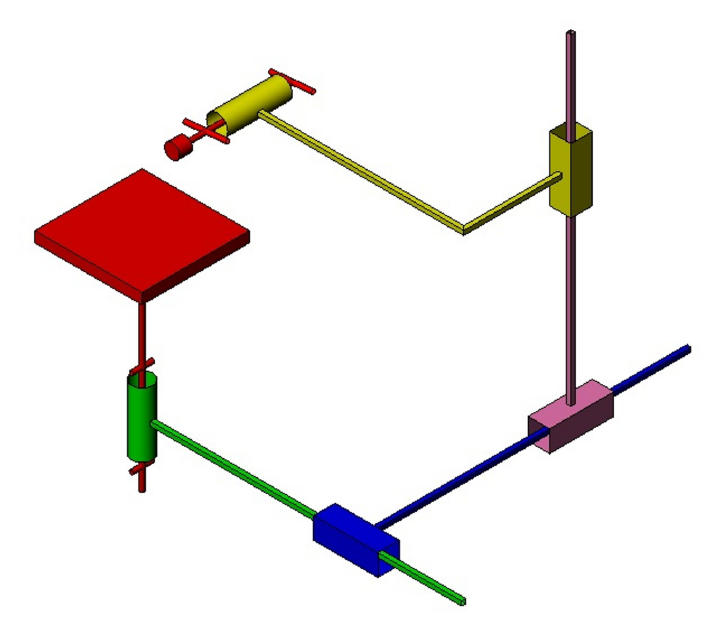
Fig. 49 Modélisation cinématique du centre 4 axes C300H#
Pour la suite, on ne tiendra pas compte de la rotation de l’outil réalisé par la broche (mouvement de coupe pour l’usinage).
\(\mathcal{R}_p=(O_p, \overrightarrow{x_p}, \overrightarrow{y_p}, \overrightarrow{z_p})\) le repère associé à la pièce posée sur le plateau;
\(\mathcal{R}_m=(O_m, \overrightarrow{x_m}, \overrightarrow{y_m}, \overrightarrow{z_m})\) le repère associé au centre d’usinage, orienté par les différents axes;
l’axe \(\overrightarrow{z_m}\) est l’axe de la broche, orienté s’éloignant de la pièce;
le point \(O_o\) est l’intersection entre l’axe de rotation B et la face supérieure du plateau.
Dans la configuration de référence du centre d’usinage (notamment l’axe \(B\) à zéro), on positionne la pièce sur le plateau tel que la base du repère pièce \(\mathcal{B}_p\) soit identique à la base machine \(\mathcal{B}_m\).
Le paramétrage du système ainsi que les matrices homogènes de transformations entre repères sont données en annexe.
Le positionnement de l’outil par rapport à la pièce est spécifié par les composantes de position et les cosinus directeurs (\(X_p,Y_p,Z_p,i,k\)).
Modèles Géométriques Direct et Inverse#
Question 1.1 : Rappeler les variables de l’espace des tâches et celles de l’espace articulaire.
Question 1.2 : À partir de la présentation du sujet et des annexes, déterminer les MGD et MGI du centre d’usinage.
On souhaite usiner un plan de longueur \(L\), avec un outil hémisphérique piloté en son centre tout en faisant varier l’orientation de l’axe outil (Fig. 50). Pour cela, on construit une trajectoire allant du premier positionnement de l’outil \(P_1\) incliné d’un angle \(\alpha\) (\(\alpha > 0\)) par rapport à \(\mathbf{z_p}\), au positionnement outil \(P_2\) incliné d’un angle \(-\alpha\).
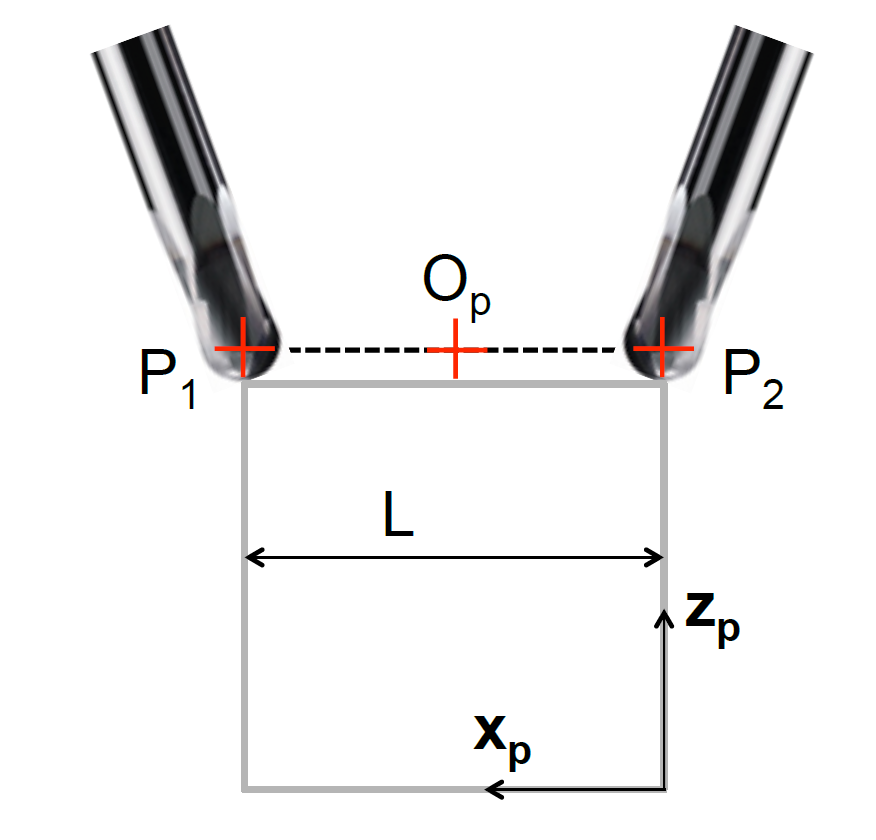
Fig. 50 Présentation des différentes configurations de l’outil.#
Question 1.3 : Pour chacun des cas \(P_1\) et \(P_2\), déterminer les valeurs des variables traduisant le positionnement de l’outil dans l’espace des tâches et dans l’espace articulaire.
Modes d’interpolation#
Question 2.1 : Pour un trajet calculé par mode d’interpolation linéaire dans l’espace des tâches, représenter en fonction de l’abscisse curviligne du trajet, l’évolution des variables des tâches. Comment évoluent qualitativement les variables articulaires ?
Question 2.2 : Faire de même pour un mode d’interpolation linéaire dans l’espace articulaire.
Pour faciliter l’écriture, on définit pour la suite le paramètre d’interpolation \(u\), variant de 0 à 1.
Question 2.3 : Exprimer les deux équations vectorielles fonction de \(u\) qui traduisent l’interpolation linéaire dans l’espace des tâches et l’espace articulaire en fonction des valeurs correspondantes associées à \(P_1\) et \(P_2\)
Influence du mode d’interpolation#
On cherche à déterminer l’effet dans l’espace des tâches du mode d’interpolation dans l’espace articulaire.
Question 3.1 : Exprimer l’écart géométrique généré au niveau du point piloté de l’outil pour toute valeur de \(u\).
Question 3.2 : Faire l’application pour \(u=0.5\) (milieu de la trajectoire). Analyser les influences des autres paramètres.
Question 3.3 : Aller au bout de l’application et effectuer une représentation du comportement pour un posage de la pièce tel que \(d_x=0\) et \(d_z=\dfrac{L}{2}\), et dans le cas où \(\alpha = 45^{\circ}\).
Annexes#
matrices homogènes de transformations entre repères issues du paramétrage
avec
(\(p_x,p_y,p_z\)) les composantes du vecteur caractéristique machine \(\mathbf{O_m O_o}\);
(\(d_x,d_y,d_z\)) les composantes du vecteur caractéristique de décalage lié au posage de la pièce sur la table \(\mathbf{O_o O_p}\);
\(j_z\) la caractéristique de longueur d’outil.
