Modèles Géométriques Inverse et Direct - Résolution

Introduction

Espace des tâches - Espace articulaire

Espace des tâches : lieu, géométriquement repéré où intervient l’effecteur pour effectuer la tâche ou opération. Cet espace est aussi nommé « espace opérationnel ». C’est un espace de dimension 6, constitué de 3 paramètres pour la position d’un point et de 3 paramètres pour l’orientation d’une base par rapport à une autre.

Espace articulaire : en robotique où un degré de liberté entre deux organes consécutifs est appelé une « articulation ». L’amplitude de ce mouvement est la valeur du « paramètre articulaire ». Cet espace est de dimension égale au nombre de degrés de liberté de la structure.

Modèles géométriques direct et inverse

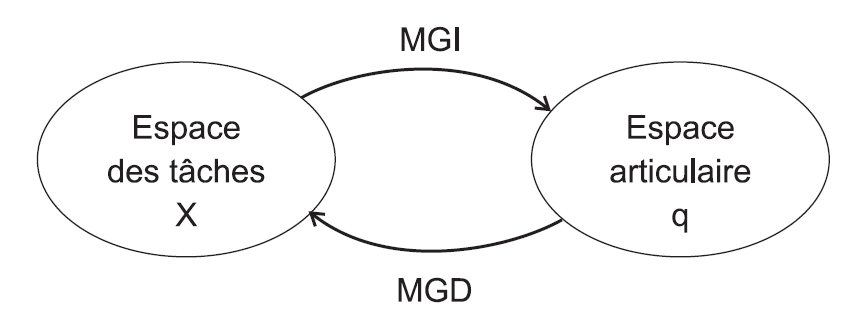
Fig. 16 Modèles géométriques direct et inverse

Le modèle géométrique direct (MGD) permet d’exprimer le positionnement de l’effecteur \(\mathbf{X} = (x_{eff}, y_{eff}, z_{eff}, \phi, \theta, \psi)\) défini dans le repère de la tâche \(\mathcal{R}_{tâche}\) en fonction de la configuration articulaire \(\mathbf{q} = (q_1, q_2, \cdots , q_n)\) commandée et des paramètres géométriques décrivant la structure \(\xi\) :

\[ \begin{equation} \mathbf{X} = \text{MGD}(\mathbf{q},\xi) \end{equation} \]

Le modèle géométrique inverse (MGI) exprime la configuration articulaire \(\mathbf{q} = (q_1, q_2, \cdots , q_n)\) commandée en fonction du positionnement de l’effecteur \(\mathbf{X} = (x_{eff}, y_{eff}, z_{eff}, \phi, \theta, \psi)\) dans le repère de la tâche et des paramètres géométriques décrivant la structure \(\xi\) :

(10)\[ \begin{equation} \mathbf{q} = \text{MGI}(\mathbf{X},\xi) \end{equation} \]

Structures sérielles

En général, la tâche est définie dans un repère spécifique \(\mathcal{R}_{tâche}\), défini pour l’opération attendue, qui est différent du repère de base du robot \(\mathcal{R}_{0}\). Le passage entre ces deux repères est construit par une matrice de transformation homogène \(\mathbf{T}_{tâche\, 0}\) dont les paramètres sont évalués par identification, après fixation relative du robot et de la zone locale d’intérêt pour la tâche.

A l’autre extrémité du robot, côté effecteur, il est utile de définir un nouveau repère lié à l’effecteur \(\mathcal{R}_{eff}\) pour programmer plus simplement les mouvements. Ainsi, la mesure de l’effecteur vis à vis de sa fixation sur l’organe terminal du robot permet d’associer une nouvelle transformation homogène \(\mathbf{T}_{n\, eff}\) entre \(\mathcal{R}_{eff}\) et le repère du corps à extrémité du robot \(\mathcal{R}_{n}\).

La transformation globale entre le repère de la tâche et le repère de l’effecteur s’écrit alors :

\[ \begin{equation} \mathbf{T}_{tâche\, eff} = \mathbf{T}_{tâche\, 0} \mathbf{T}_{0n}(q) \mathbf{T}_{n\, eff} \end{equation} \]

Pour un robot permettant de positionner librement l’effecteur dans l’espace, il est possible d’inverser la relation précédente, les transformations \(\mathbf{T}_{tâche\, 0}\) et \(\mathbf{T}_{n\, eff}\) étant des constantes saisie dans le contrôleur du robot :

(11)\[ \begin{equation} \mathbf{T}_{0n}(q) = \mathbf{T}_{tâche\, 0}^{-1} \mathbf{T}_{tâche\, eff} \mathbf{T}_{n\, eff}^{-1} \end{equation} \]

Pour réaliser le positionnement souhaité de l’effecteur dans le repère de la tâche, le problème consiste alors à trouver les différentes valeurs des variables articulaires \(q\), c’est à dire le membre de gauche de l’équation (11).

Pour les structures sérielles, le MGD est obtenu directement lors du paramétrage de la géométrie et des liaisons. Le Modèle géométrique inverse nécessite lui d’extraire les variables articulaires de chaque transformation pour les exprimer directement en fonction de la tâche à accomplir. Pour cela, différentes solutions sont classiquement utilisées, choisies en fonction de la structure et de sa complexité.

D’un point de vue pratique, il peut exister plusieurs solutions \(\mathbf{q}_i\) à l’équation (10). Cela correspond alors aux différentes configurations articulaires permettant de réaliser le même positionnement de l’effecteur dans le référentiel de base. La figure Fig. 17 présente les 4 solutions du MGI pour un robot sériel de type 5 axes (5R).

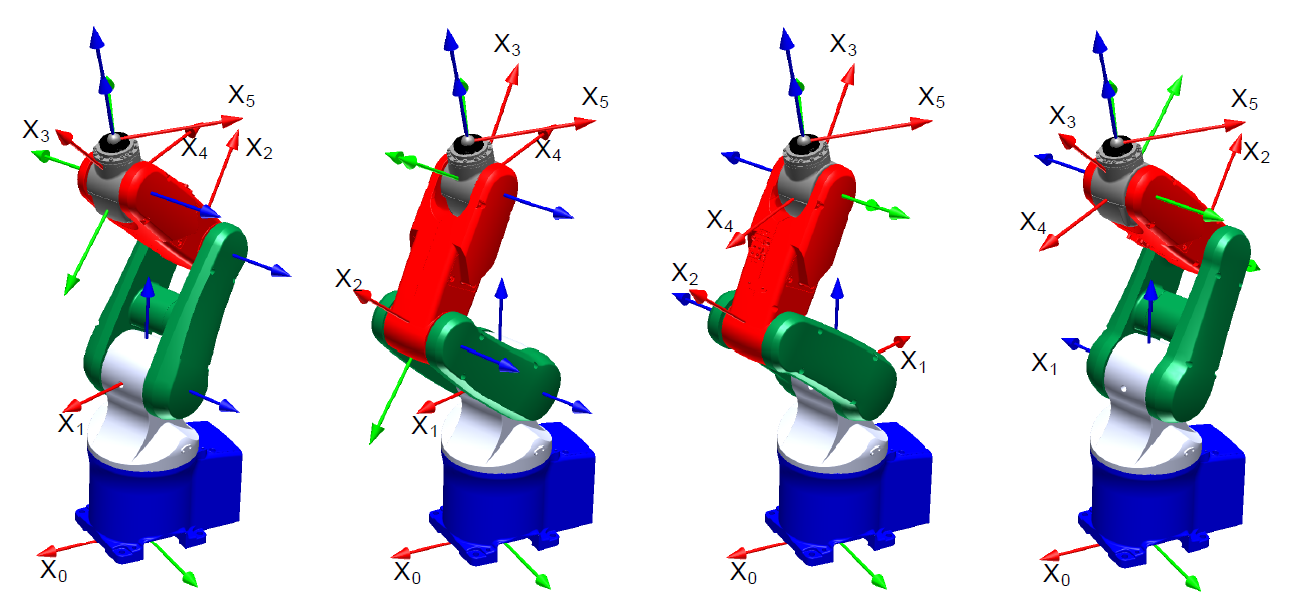
Fig. 17 Les 4 configurations articulaires solutions du MGI pour un même positionnement de l’effecteur - robot 5R Denso VP5243

Calcul trigonométrique simple

Pour les structures relativement simples possédant moins de six liaisons ou restant dans un plan, il est possible d’exprimer directement les MGI et MGD par construction géométrique et trigonométrique sans avoir à définir de façon explicite toutes les transformations entre repère associés aux différents corps. Les astuces de résolution consistent alors à isoler les variables articulaires puis à les résoudre à l’aide des relations trigonométriques usuelles.

Méthode de Paul

Soit un robot de structure ouverte simple possédant n corps et liaisons. La modélisation géométrique abouti à une transformation homogène globale de la forme :

\[ \begin{equation} \mathbf{T}_{0n}(q) = \mathbf{T}_{01}(q_1) \mathbf{T}_{12}(q_2) \mathbf{T}_{23}(q_3) \cdots \mathbf{T}_{(n-1)n}(q_n) \end{equation} \]

Le positionnement de l’effecteur est connu ; ramené au positionnement du dernier corps du robot, il est possible de l’exprimer dans la base du robot à l’aide de l’équation (11) :

\[\begin{split} \begin{equation} ^0 \mathbf{X} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & P_x \\ r_{21} & r_{22} & r_{23} & P_y \\ r_{31} & r_{32} & r_{33} & P_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{equation} \end{split}\]

Résoudre le modèle géométrique inverse revient à résoudre l’équation (12) en \(q\) :

(12)\[ \begin{equation} ^0 \mathbf{X} = \mathbf{T}_{01}(q_1) \mathbf{T}_{12}(q_2) \mathbf{T}_{23}(q_3) \cdots \mathbf{T}_{(n-1)n}(q_n) \end{equation} \]

La méthodologie proposée par Paul consiste à multiplier successivement à gauche les deux membres de l’équation (12) par les matrices \(\mathbf{T}_{ii-1}(q_i)\), pour \(i\) variant de \(1\) à \(n-1\). Ainsi, les variables articulaires se trouvent isolées une à une dans le membre de gauche, tandis que le membre de droite peut être exprimé à partir du MGD.

(13)\[ \begin{equation} \mathbf{T}_{10}(q_1)\ ^0 \mathbf{X} = \mathbf{T}_{12}(q_2) \mathbf{T}_{23}(q_3) \cdots \mathbf{T}_{(n-1)n}(q_n) \end{equation} \]

L’identification terme à terme de l’équation (13) permet d’isoler une à deux équations scalaires faisant intervenir uniquement la variable articulaire \(q_1\) ainsi que des constantes géométriques du système et les paramètres du positionnement de l’effecteur \(^0 X\). En procédant de proche en proche, la méthode mène aux équations suivantes :

\[\begin{split} \begin{align*} \mathbf{T}_{10}(q_1)\ ^0 \mathbf{X} &= \mathbf{T}_{12}(q_2) \mathbf{T}_{23}(q_3) \cdots \mathbf{T}_{(n-1)n}(q_n) \\ \mathbf{T}_{21}(q_2) \mathbf{T}_{10}(q_1)\ ^0 \mathbf{X} &= \mathbf{T}_{23}(q_3) \cdots \mathbf{T}_{(n-1)n}(q_n) \\ \vdots \\ \mathbf{T}_{(n-1)(n-2)}(q_{(n-1)}) \cdots \mathbf{T}_{21}(q_2) \mathbf{T}_{10}(q_1)\ ^0 \mathbf{X} &= \mathbf{T}_{(n-1)n}(q_n) \end{align*} \end{split}\]

La forme de chacune des équation scalaire obtenue peut être résolue de façon plus ou moins simple. Ces équations sont classés en type, selon leur forme.

Méthode de Pieper

Cette méthode est particulièrement adaptée aux structures dites « découplables », c’est à dire, dont le problème de résolution du MGI peut être traité en deux sous problèmes à trois inconnues chacun. Pour un robot à 6 axes, il s’agit de structures comportant :

• soit trois liaisons pivot successives d’axe concourants formant ainsi une rotule. Il s’agit par exemple des structures de type XXX(RRR), XX(RRR)X, X(RRR)X … (où R représente une liaison pivot, et X une liaison pivot ou rotule)

• soit trois liaisons glissière (pas automatiquement successives) : PPPRRR, PPRPRR, PRPRPR … (où P représente une liaison glissière)

Cette méthode conduit à résoudre des équations de type 1, 2, 3, 9, 10 et 11 (paragraphe D).

Principe de résolution pour des robots avec poignet

Le centre du poignet est l’intersection des axes de rotation concourants des trois dernières liaisons pivots du robot présentant cette particularité (Fig. 18).

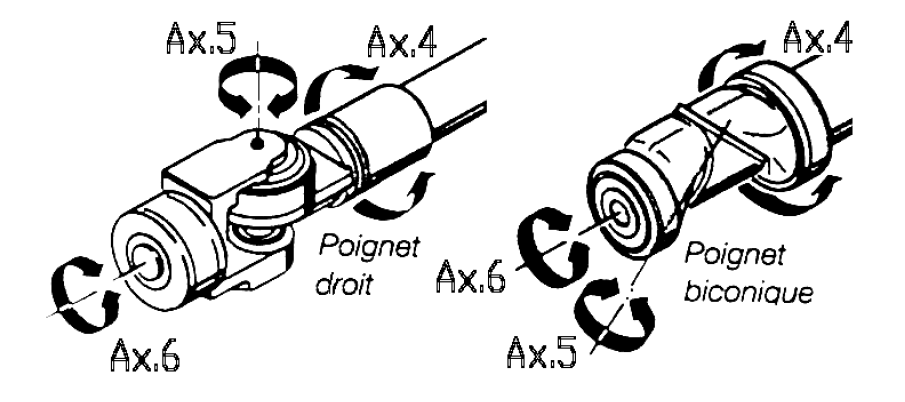
Fig. 18 Exemple structures de poignets à trois articulations concourantes

La position de ce point caractéristique ne dépend donc que des trois premières variables articulaires \(q_1\), \(q_2\) et \(q_3\). Il y a donc un découplage entre la position de ce point caractéristique et l’orientation du poignet. Le problème peut donc se séparer en deux problèmes à 3 équations et 3 inconnues.

1 - Équation en position : Dans la structure de type poignet, l’origine du repère \(\mathcal{R}_6\) lié au dernier corps peut être directement positionnée au centre de la rotule. Si ce n’est pas le cas, il faut prendre en compte la transformation de ce dernier corps pour passer par exemple de la face extrémité pour l’assemblage de l’organe terminal vers le centre de la rotule. Soit \(^0 \mathbf{X}_{rot}\) le positionnement à respecter pour le dernier corps solide, positionné par le centre de la rotule et exprimé dans le référentiel de base du robot :

\[\begin{split} \begin{equation} ^0 \mathbf{X}_{rot} = \begin{bmatrix} & & & P_x \\ & \mathbf{R}_{rot} & & P_y \\ & & & P_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{equation} \end{split}\]

Cette origine, par définition de la rotule, est également origine du repère \(\mathcal{R}_4\) associé au quatrième corps :

\[\begin{split} \begin{equation} \begin{bmatrix} P_{x\ rot} \\ P_{y\ rot} \\ P_{z\ rot} \\ 1 \end{bmatrix} = \ ^0 \mathbf{P}_6 = \ ^0 \mathbf{P}_4 \end{equation} \end{split}\]

Ce qui permet d’exprimer plus rapidement le lien entre les trois premières variables articulaires et la position :

\[\begin{split} \begin{equation} \begin{bmatrix} P_{x\, rot} \\ P_{y\, rot} \\ P_{z\, rot} \\ 1 \end{bmatrix} = \mathbf{T}_{01}(q_1) \mathbf{T}_{12}(q_2) \mathbf{T}_{23}(q_3) \mathbf{T}_{34}(q_4) \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \end{equation} \end{split}\]

Pour terminer la résolution, de façon identique à la méthode de Paul, on multiplie successivement à gauche les membres de l’équation par \(\mathbf{T}_{i(i-1)}(q_i)\), pour \(i\) variant de 1 à 2. L’identification terme à terme des deux matrices permet de déterminer successivement les variables \(q_1\) puis \(q_2\) puis \(q_3\).

2 - Équation en orientation :

Une fois les trois premières variables articulaires évaluées, il ne reste qu’à écrire la contrainte sur l’orientation à donner à l’effecteur par la rotule. En effet, la position du centre rotule étant réalisée, le troisième corps possède alors une orientation imposée. Les trois dernières variables associées au poignet sont donc les angles \(\theta_4\), \(\theta_5\) et \(\theta_6\) permettant alors de passer de l’orientation du troisième corps à celle du sixième :

\[\begin{split} \begin{align*} \mathbf{R}_{rot} &= \mathbf{R}_{06}(q_1, q_2, q_3, \theta_4, \theta_5, \theta_6) \\ \Leftrightarrow \mathbf{R}_{03}(q_1, q_2, q_3) \mathbf{R}_{rot} &= \mathbf{R}_{36}(\theta_4, \theta_5, \theta_6) \\ \Leftrightarrow \mathbf{R}_{eq} &= \mathbf{R}_{34}(\theta_4) \mathbf{R}_{45}(\theta_5) \mathbf{R}_{56}(\theta_6) \end{align*} \end{split}\]

Le membre de gauche \((\mathbf{R}_{eq})\) étant connu, il ne reste donc plus qu’à identifier successivement terme à terme les matrices après multiplication à gauche par \(\mathbf{R}_{i(i-1)}(q_i)\), pour \(i\) variant de 4 à 5 pour extraire les valeurs des angles \(\theta_4\), \(\theta_5\) et \(\theta_6\).

Quelques autres méthodes…

Parmi les autres méthodes existantes, on peut citer deux autres techniques usuelles :

Méthode de Raghavan et Roth

Cette méthode est basée sur la résolution d’un système d’équations non linéaires baptisée « élimination dyalitique ». Elle consiste à déterminer au travers d’un polynôme nommé « polynôme caractéristique » toutes les solutions possibles du MGI par le calcul des valeurs correspondantes d’une première variable articulaire. Les variables articulaires suivantes sont déterminées alors pour chaque cas de façon unique.

Méthode numérique

Parmi les méthodes numériques, on retiendra l’algorithme de Newton-Raphson, extension de la méthode de Newton. Par itérations successives, elle permet de résoudre un système d’équations (non linéaires) en recherchant les zéros de fonctions continûment dérivables. Soit \(\mathbf{X}^*\) la configuration connue que le robot doit atteindre par les valeurs articulaires \(\mathbf{q}^*\) qui sont à déterminer. L’inversion du modèle direct :

\[ \begin{equation} \mathbf{X} = \text{MGD}(\mathbf{q}) \end{equation} \]

est obtenue par en utilisant la matrice jacobienne \(\mathbf{J}\) (voir paragraphe~\ref{5.2}), comme linéarisation du modèle inverse au point d’itération \(k\). Les variables articulaires estimées à l’itération suivante \(k + 1\) sont données par :

\[ \begin{equation} \mathbf{q}^{k+1} - \mathbf{q}^k = \mathbf{J}^{-1} (\mathbf{q}^k ) (\mathbf{X}^* - \mathbf{X}^k) \end{equation} \]

Une difficulté des méthodes numériques est d’assurer une convergence, particulièrement sensible à l’initialisation.

Structures parallèles

Résolution du MGD

Dans le cas des structures parallèles, le MGD est bien plus difficile à obtenir que pour les structures sérielles. Pour cela, on utilise des méthodes numériques d’optimisation de type « Newton-Raphson » pour résoudre le système d’équations non linéaires formé par la relation de fermeture géométrique donnée en équation (9).

Résolution du MGI

Les variables articulaires \(q_i\) se déterminent indépendamment les unes des autres. Le MGI doit aboutir à une équation scalaire pour chaque variable articulaire :

\[ \begin{equation} q_i = \text{MGI}(\mathbf{X},\xi) \end{equation} \]

Le MGI global est alors formé à partir de toutes les équations :

\[ \begin{equation} \mathbf{q} = \text{MGI}(\mathbf{X},\xi) \end{equation} \]

Écriture vectorielle

L’équation 3.5 de fermeture géométrique peut se réécrire :

\[ \begin{equation} q_i \frac{\overrightarrow{A_i B_i}}{\lVert \overrightarrow{A_i B_i} \rVert} = \overrightarrow{A_i O_m}_{\mathcal{B}_m} + \overrightarrow{O_m O_p}_{\mathcal{B}_m} + \mathbf{R}_{mp} \overrightarrow{0_p B_i}_{\mathcal{B}_p} \end{equation} \]

où les paramètres géométriques constants \(\xi\) liés aux jambes sont inclus dans le terme \(q_i\). Ainsi,

\[ \begin{equation} q_i^2 = \lVert \overrightarrow{A_i O_m}_{\mathcal{B}_m} + \overrightarrow{O_m O_p}_{\mathcal{B}_m} + \mathbf{R}_{mp} \ \overrightarrow{0_p B_i}_{\mathcal{B}_p} \rVert^2 \end{equation} \]

Écriture matricielle

Sous forme de transformations homogènes, ce problème peut s’écrire de la façon suivante : connaissant la transformation \(\mathbf{T}_{mp}\) passant du repère fixe \(\mathcal{R}_m\) au repère de la plateforme mobile \(\mathcal{R}_p\), ainsi que les expressions des positions des points \(B_i\) dans \(\mathcal{R}_p\) (\(^p\mathbf{B}_i\)) et \(A_i\) dans \(\mathcal{R}_m\) (\(^m\mathbf{A}_i\)), les coordonnées des points \(B_i\) dans \(\mathcal{R}_m\) se calculent par :

\[\begin{split} \begin{equation} ^m \mathbf{P}_{B_i} = \mathbf{T}_{mp} \ ^p \mathbf{P}_{B_i} \quad \text{avec} \quad \ ^m \mathbf{P}_{B_i} = \begin{bmatrix} ^m \mathbf{B}_{i} \\ 1 \end{bmatrix} \quad \text{et} \quad\ ^p \mathbf{P}_{B_i} = \begin{bmatrix} ^p \mathbf{B}_{i} \\ 1 \end{bmatrix} \end{equation} \end{split}\]

La caractéristique articulaire \(q_i\) s’obtient par la relation :

\[\begin{split} \begin{align} q_i^2 &= \mathbf{A}_i \mathbf{B}_i^t \mathbf{A}_i \mathbf{B}_i \\ &= (\ ^m \mathbf{P}_{B_i} - \ ^m \mathbf{P}_{A_i} )^t (\ ^m \mathbf{P}_{B_i} - \ ^m \mathbf{P}_{A_i} ) \\ &= (\mathbf{T}_{mp} \ ^p \mathbf{P}_{B_i} - \ ^m \mathbf{P}_{A_i} )^t (\mathbf{T}_{mp} \ ^p \mathbf{P}_{B_i} - \ ^m \mathbf{P}_{A_i} ) \quad \text{où} \quad \ ^m \mathbf{P}_{A_i} = \begin{bmatrix} ^m \mathbf{A}_{i} \\ 1 \end{bmatrix} \\ \end{align} \end{split}\]

Remarque

Pour les structures hybrides, il est possible de coupler les deux approches :

• Denavit-Hartenberg pour la partie sérielle,

• Merlet pour la partie parallèle.