Correction de l’examen de Système Poly-Articulés - 2022/2023

On s’intéresse aux robots xArm. Il s’agit d’une gamme de robots composés de 3 modèles : xArm5, xArm6 et xArm7. Le numéro indique le nombre de liaisons pivots du robot. La figure Fig. 75 présente le robot xARm7. La Fig. 72 présente les 3 modèles de robot avec les différentes articulations.

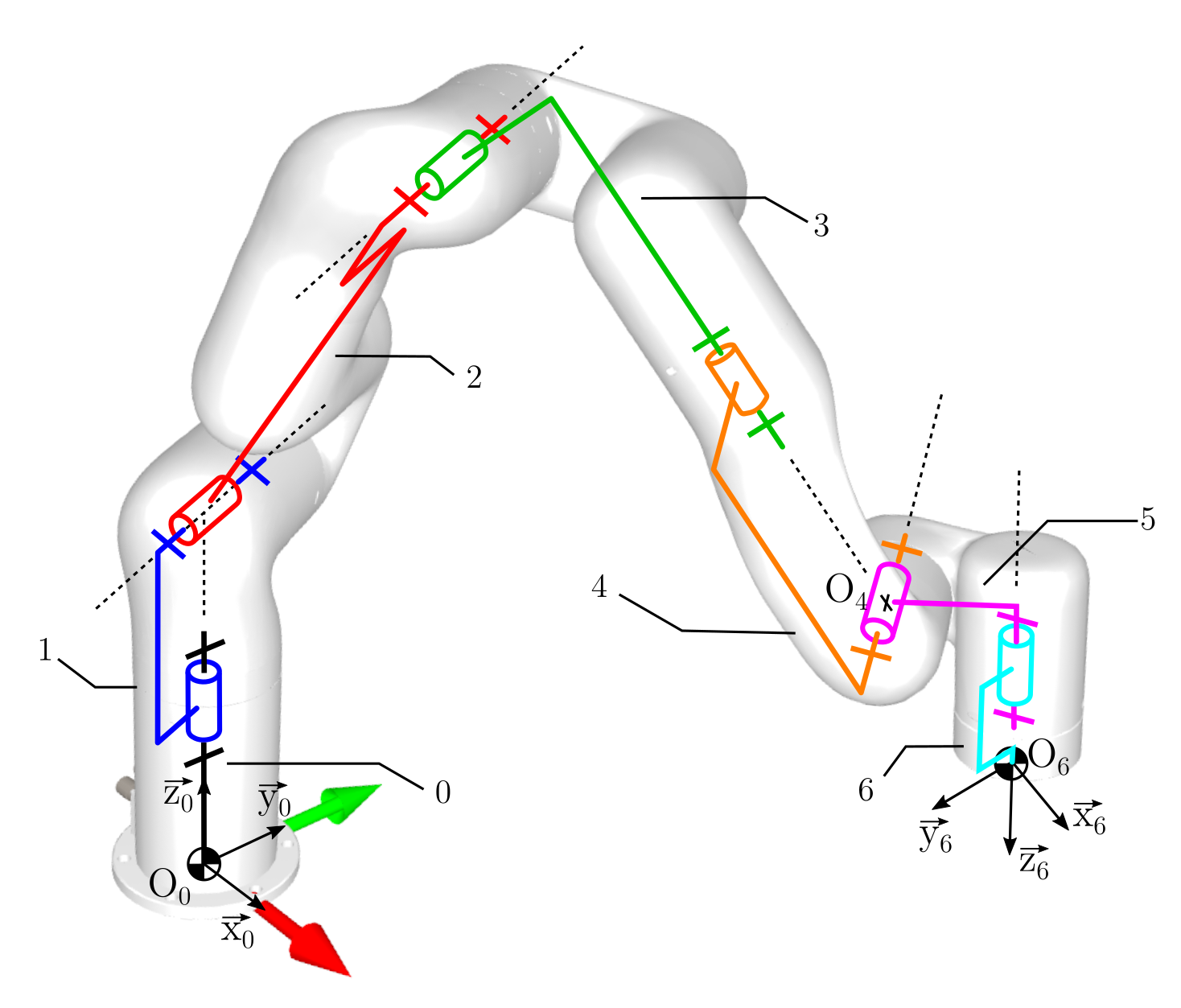
Fig. 75 Robot xArm7

Paramétrage : xArm6

Dans un premier temps, on s’intéresse uniquement au robot xArm6 composé de 6 liaisons pivots (cf. Fig. 76) sans tenir compte de la pince. Le schéma cinématique de ce robot est fourni dans le Document Réponse A.

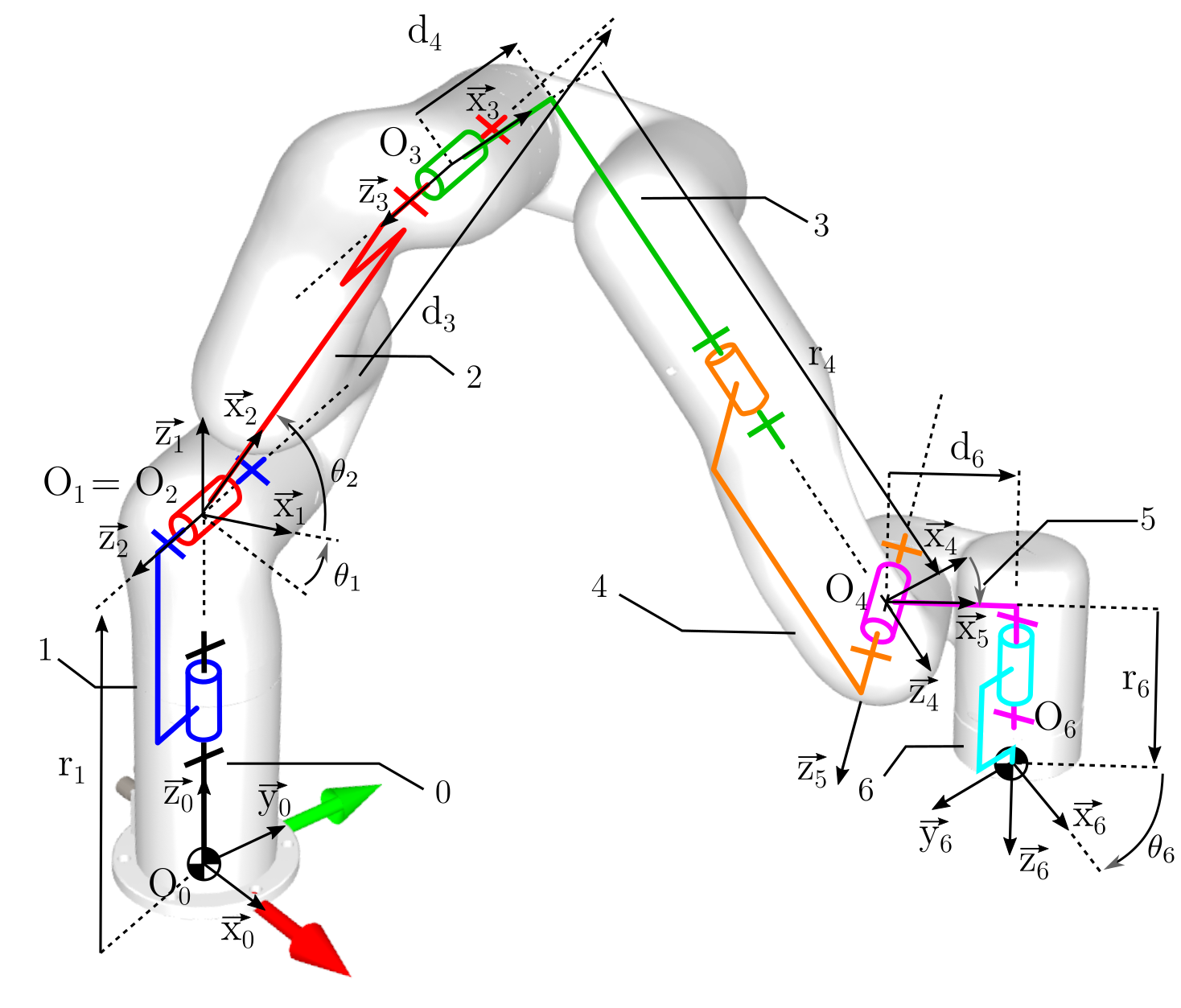
Question 1.1 : Construire sur le Document Réponse A le paramétrage du robot au sens de Denavit Hartenberg modifié (DHm) en partant du repère de base 0 déjà fourni. Le point \(O_4\) est déjà positionné.

Solution

Question 1.2 : Synthétiser les résultats dans le tableau DHm associé. Dessiner également les figures de changement de repère en représentant les différents paramètres articulaires comme étant positif.

Solution

Tableau de paramètres DHm pour le robot

	\(d_i\)	\(\alpha_i\)	\(r_i\)	\(\theta_i\)
\(\mathbf{T}_{01}\)	0	0	\(r_1\)	\(\theta_1\)
\(\mathbf{T}_{12}\)	0	\(90^{\circ}\)	0	\(\theta_2\)
\(\mathbf{T}_{23}\)	\(d_3\)	0	0	\(\theta_3\)
\(\mathbf{T}_{34}\)	\(d_4\)	\(90^{\circ}\)	\(r_4\)	\(\theta_4\)
\(\mathbf{T}_{45}\)	0	\(-90^{\circ}\)	0	\(\theta_5\)
\(\mathbf{T}_{56}\)	\(d_6\)	\(90^{\circ}\)	\(r_6\)	\(\theta_6\)

Question 1.3 : Quels sont les paramètres de l’espace des tâches et les paramètres de l’espace articulaire ?

Solution

Les paramètres articulaires sont au nombre de 6 il s’agit des 6 paramètres \(\theta_i \, \ i = 1..6\). Les paramètres de l’espaces des tâches correspondent à la position de l’effecteur et à l’orientation de celui-ci dans le repère \(\mathcal{R}_6\). Autrement dit il sont au nombre de 3 pour la position et au nombre de 3 ou 4 pour l’orientation suivant le paramétrage (Euler, Bryant, Quaternion) choisi.

Modèle Géométrique Direct : xArm6

Étant donné le nombre de paramètres articulaires conséquent, on s’intéressera uniquement aux 4 premières liaisons. Les 2 dernières liaisons (5 et 6 sur le robot xArm6) étant communes aux 3 modèles xArm5, xArm6 et xArm7.

Question 2.1 : Déterminer les matrices homogènes de transformation \(T_{01}\), \(T_{12}\), \(T_{23}\) et \(T_{34}\) entre les différents corps.

Solution

Matrices homogènes élémentaires de transformations entre repères : $\( \begin{align*} \mathbf{T}_{01}&= \begin{bmatrix} \text{C}\theta_1 & -\text{S}\theta_1 & 0 & 0 \\ \text{S}\theta_1 & \text{C}\theta_1 & 0 & 0 \\ 0 & 0 & 1 & r_1 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{12}&= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \text{C}\alpha_2 & -\text{S}\alpha_2 & 0 \\ 0 &\text{S}\alpha_2 & \text{C}\alpha_2 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \times \begin{bmatrix} \text{C}\theta_2 & -\text{S}\theta_2 & 0 & 0 \\ \text{S}\theta_2 & \text{C}\theta_2 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{12}&= \begin{bmatrix} \text{C}\theta_2 & -\text{S}\theta_2 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ \text{S}\theta_2 & \text{C}\theta_2 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{23}&= \begin{bmatrix} \text{C}\theta_3 & -\text{S}\theta_3 & 0 & d_3 \\ \text{S}\theta_3 & \text{C}\theta_3 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{34}&= \begin{bmatrix} 1 & 0 & 0 & d_4 \\ 0 & \text{C}\alpha_4 & -\text{S}\alpha_4 & 0 \\ 0 &\text{S}\alpha_4 & \text{C}\alpha_4 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \times \begin{bmatrix} \text{C}\theta_4 & -\text{S}\theta_4 & 0 & 0 \\ \text{S}\theta_4 & \text{C}\theta_4 & 0 & 0 \\ 0 & 0 & 1 & r_4 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{34}&= \begin{bmatrix} \text{C}\theta_2 & -\text{S}\theta_2 & 0 & d_4 \\ 0 & 0 & -1 & -r_4 \\ \text{S}\theta_2 & \text{C}\theta_2 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{align*} \)$

Question 2.2 : En utilisant les résultats précédents, déterminer l’expression du modèle géométrique direct (MGD) permettant d’exprimer la position du point \(O_4\) dans le repère de base du robot.

Solution

On cherche a déterminer le MGD aussi en position du point \(O_4\). On note \((x, y, z)\) ses coordonnés dans le repère \(\mathcal{R}_0\)

\[\begin{split} \begin{align*} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} &= \mathbf{T}_{01} \cdot \mathbf{T}_{12} \cdot \mathbf{T}_{23} \cdot \mathbf{T}_{34} \cdot \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \\ \\ \begin{pmatrix} X \\ Y \\Z \\ 1 \end{pmatrix} &= \mathbf{T}_{01} \cdot \mathbf{T}_{12} \cdot \mathbf{T}_{23} \cdot \begin{pmatrix} d_4 \\-r_4 \\ 0 \\ 1 \end{pmatrix} \\ \\ \begin{pmatrix} X \\ Y \\ Z \\ 1 \end{pmatrix} &= \mathbf{T}_{01} \cdot \mathbf{T}_{12} \cdot \begin{pmatrix} d_3 + d_4 \text{C}(\theta_3) + r_4\text{S}(\theta_3) \\ d_4\text{S}(\theta_3) - r_4\text{C}(\theta_3) \\ 0 \\ 1 \end{pmatrix}\\ \\ \begin{pmatrix} X \\ Y \\ Z \\ 1 \end{pmatrix} &= \mathbf{T}_{01} \cdot \begin{pmatrix} d_4\text{C}(\theta_2 + \theta_3) + r_4\text{S}(\theta_2 + \theta_3) + d_3\text{C}(\theta_2) \\ 0 \\ d_4\text{S}(\theta_2 + \theta_3) - r_4\text{C}(\theta_2 + \theta_3) + d_3\text{S}(\theta_2) \\ 1 \end{pmatrix}\\ \\ \begin{pmatrix} X \\ Y \\ Z \\ 1 \end{pmatrix} &= \begin{pmatrix} \text{C}(\theta_1)(d_4\text{C}(\theta_2 + \theta_3) + r_4\text{S}(\theta_2 + \theta_3) + d_3\text{C}(\theta_2)) \\ \text{S}(\theta_1)(d_4\text{C}(\theta_2 + \theta_3) + r_4\text{S}(\theta_2 + \theta_3) + d_3\text{C}(\theta_2)) \\ r_1 - r_4\text{C}(\theta_2 + \theta_3) + d_4\text{S}(\theta_2 + \theta_3) + d_3\text{S}(\theta_2) \\ 1 \end{pmatrix} \end{align*} \end{split}\]

Fig. 76 Robot xArm 5, 6 et 7. Visualisations des liaisons pivots

Modèle Géométrique Inverse : xArm6

Dans cette partie (sauf Question 3.5) on s’intéresse, comme précédemment, uniquement à la position du point \(O_4\).

Question 3.1 : Donner la définition du Modèle Géométrique Inverse (MGI) d’un système poly-articulé.

Solution

Le modèle géométrique inverse d’un système correspond à une fonction mathématique permettant d’exprimer les paramètres articulaires du système en fonction des paramètres de l’espace des taches qui eux sont connus.

Question 3.2 : Donner sans faire de calcul le nombre de solutions du MGI en position du point \(0_4\). Illustré rapidement cela par des schémas.

Solution

Le nombre de solution du MGI en position du point \(O_4\) est des 4. Effectivement, 4 configurations articulaires différentes permettent d’atteindre le point \(0_4\). Le premier dédouble correspond au renversement des bras 2 et 3. et le deuxième dédoublement correspond au configurations ou \(\theta_1\) est tourné de 180 deg.

Question 3.3 : Détailler de manière qualitative la méthode/la démarche permettant de résoudre le MGI en position du point \(O_4\) dans ce système.

Solution

Pour résoudre le MGI d’un système sérielle ont utilise la méthode de Paul. Cette méthode consiste a déterminer les \(\theta_i\) de proche en proche en compensant par \(\theta_1\). Pour cela on multiplie chaque terme de l’équation suivante par \(\mathbf{T}_{01}^{-1}\).

\[\begin{split} \begin{equation} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} = \mathbf{T}_{01} \cdot \mathbf{T}_{12} \cdot \mathbf{T}_{23} \cdot \mathbf{T}_{34} \cdot \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \\ \end{equation} \end{split}\]

Cela permet d’isoler \(\theta_1\) et de trouver ainsi une équation remarque parmi les équations de type afin d’identifier une ou plusieurs solution pour \(\theta_1\). Un fois \(\theta_1\) déterminé, on réitère en multipliant de chaque coté par \(\mathbf{T}_{12}^{-1}\) et ainsi de suite jusqu’à trouvé tous les \(\theta_i\).

Question 3.4 : Mettre en œuvre cette démarche en vous appuyant sur les équations données en Annexe. Il n’est pas demandé d’effectuer tous les calculs, mais plutôt de conduire la démarche. Il est également fortement conseillé de faire des changements de variable lors de la résolution pour gagner du temps. Déterminer ainsi le nombre de solutions du MGI.

Solution

Le paramètre \(\theta_4\) n’apparaissant pas dans le MGD, on aura besoin des matrices inverses \(\mathbf{T}_{10}\) et \(\mathbf{T}_{21}\)

\[\begin{split} \begin{align*} \mathbf{T}_{10}&= \begin{bmatrix} \text{C}\theta_1 & \text{S}\theta_1 & 0 & 0 \\ -\text{S}\theta_1 & \text{C}\theta_1 & 0 & 0 \\ 0 & 0 & 0 & -r_1 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{21}&= \begin{bmatrix} \text{C}\theta_2 & 0 & \text{S}\theta_2 & 0 \\ -\text{S}\theta_2 & 0 & \text{C}\theta_2 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{align*} \end{split}\]

Résolution en utilisant la méthode de Paul :

1 - Première étape :

\[\begin{split} \begin{align*} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} &= \mathbf{T}_{01} \cdot \mathbf{T}_{12} \cdot \mathbf{T}_{23} \cdot \mathbf{T}_{34} \cdot \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \\ \\ \mathbf{T}_{10} \cdot \begin{pmatrix} X \\ Y \\ Z \\ 1 \end{pmatrix} &= \begin{pmatrix} d_4\text{C}(\theta_2 + \theta_3) + r_4\text{S}(\theta_2 + \theta_3) + d_3\text{C}(\theta_2) \\ 0 \\ d_4\text{S}(\theta_2 + \theta_3) - r_4\text{C}(\theta_2 + \theta_3) + d_3\text{S}(\theta_2) \\ 1 \end{pmatrix}\\ \\ \begin{pmatrix} X \text{C}(\theta_1) + Y \text{S}(\theta_1) \\ -X \text{S}(\theta_1) + Y \text{C}(\theta_1) \\ -r_1 \\ 1 \end{pmatrix} &= \begin{pmatrix} d_4\text{C}(\theta_2 + \theta_3) + r_4\text{S}(\theta_2 + \theta_3) + d_3\text{C}(\theta_2) \\ 0 \\ d_4\text{S}(\theta_2 + \theta_3) - r_4\text{C}(\theta_2 + \theta_3) + d_3\text{S}(\theta_2) \\ 1 \end{pmatrix} \end{align*} \end{split}\]

La seconde équation du système dépend uniquement de \(\theta_1\). Cette équation correspond à une équation de type 2 (cf. annexe) avec \(X = -X\), \(Y = Y\) et \(Z = 0\) Cette équation admet deux solutions avec \(\varepsilon = \pm 1\) (cf. annexe)

2 - Deuxième étape :

La variable articulaire \(\theta_1\) est maintenant connue. Pour simplifier les notations on pose donc : \(a = X \text{C}(\theta_1) + Y \text{S}(\theta_1)\) et \(b = -X \text{S}(\theta_1) + Y \text{C}(\theta_1)\)

\[\begin{split} \begin{align*} \mathbf{T}_{21} \cdot \begin{pmatrix} a \\ b \\ -r_1 \\ 1 \end{pmatrix} &= \mathbf{T}_{23} \cdot \mathbf{T}_{34} \cdot \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \\ \\ \begin{pmatrix} a\text{C}(\theta_2) -r_1\text{S}(\theta_2) \\ -a\text{S}(\theta_2) -r_1\text{C}(\theta_2) \\ -b \\ 1 \end{pmatrix} &= \begin{pmatrix} d_3 + d_4 \text{C}(\theta_3) + r_4\text{S}(\theta_3) \\ d_4\text{S}(\theta_3) - r_4\text{C}(\theta_3) \\ 0 \\ 1 \end{pmatrix} \qquad \qquad \begin{matrix} (1) \\ (2) \\ ~ \\ ~ \end{matrix} \end{align*} \end{split}\]

Les équations (1) et (2) du système doivent judicieusement être mis au carré pour supprimer \(\theta_3\) …

Question 3.5 : S’il l’on souhaite déterminer le MGI en position et en orientation (repère 6) du système complet, est-il possible de découpler le problème en position et en orientation ? Explicité pourquoi ?

Solution

Ici il n’est pas possible de découpler le problème de position et d’orientation si l’on souhaite résoudre le MGI. Effectivement pour cela il faudrait avoir un poignet en bout de bras (3 liaisons consécutive d’axe sécant). Ici ce n’est pas le cas donc la résolution du MGI en position et en orientation ne peu pas être découplé.

Autres questions

On s’intéresse maintenant au paramétrage en orientation de l’effecteur : expression du repère \(\mathcal{R}_6\) dans le repère de base \(\mathcal{R}_0\).

Question 4.1 : Au regard de la Fig. 77 dire de quel type de paramétrage il s’agit (Euler, Bryan, Quaternion, intrinsèque, extrinsèque …). Justifier votre choix.

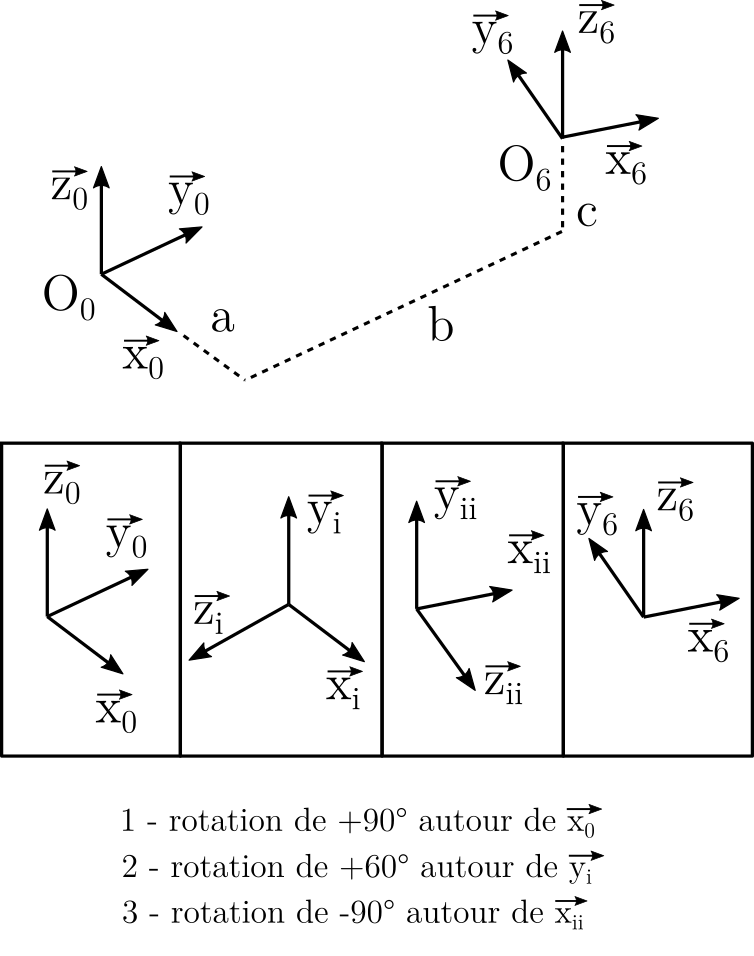
Fig. 77 Paramétrage de l’effecteur

Solution

Il s’agit ici d’un paramétrage d’Euler intrinsèque. Euler car la première et troisième rotation sont effectués autour d’un « même axe » ici \(x\). Et intrinsèque car on tourne autour des bases nouvelement créée et pas autour des axes de la première base.

Question 4.2 : Établir la matrice homogène permettant de passer du \(\mathcal{R}_6\) au repère de base \(\mathcal{R}_0\).

Solution

\[\begin{split} \begin{align*} \mathbf{R}_{0i} &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{bmatrix} \\ \\ \mathbf{R}_{i,ii} &= \begin{bmatrix} 1/2 & 0 & \sqrt{3}/2 \\ 0 & 1 & 0 \\ -\sqrt{3}/2 & 0 & 1/2 \\ \end{bmatrix} \\ \\ \mathbf{R}_{0i} &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \\ \end{bmatrix} \\ \\ \mathbf{T}_{i6} &= \begin{bmatrix} 1/2 & -\sqrt{3}/2 & 0 & a \\ \sqrt{3}/2 & -1/2 & 0 & b \\ 0 & 0 & 1 & c \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \end{align*} \end{split}\]

Question 4.3 : Expliciter les différences entre les versions 5, 6 et 7 du robot au regard des questions d’accessibilité en position et orientation.

Solution

La version 6 possède autant de paramètres articulaires que de paramètres de l’espace des taches cela permet dans un espace donnée d’atteindre n’importe quel configuration du repère \(\mathcal{R}_6\). Pour ce même espace si l’on enlève une liaison au système alors toutes les configurations ne sont plus atteignable. Enfin le système xArm7 est dit redondant car la septième liaison pivot n’apporte que très peu d’avantage et complexifie la commande car elle augmente le nombre de solution du MGI du système.

Annexes

Équations :

Inverse d’une matrice homogène :

\[\begin{split} \begin{equation*} \mathbf{T}_{ij} = \begin{bmatrix} & & & \\ & \mathbf{R}_{ij} & & \mathbf{t}_{ij} \\ & & & \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \longrightarrow \mathbf{T}_{ji} = \begin{bmatrix} & & & \\ & \mathbf{R}_{ij} ^t & & -\mathbf{R}_{ij} ^t \mathbf{t}_{ij} \\ & & & \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{equation*} \end{split}\]

Solutions de l’équation de type 2 :

\[ \begin{equation*} X \text{S}\theta_i + Y \text{C}\theta_i = Z \end{equation*} \]

Solution :

\[\begin{split} \begin{align*} \theta_i = \begin{cases} \text{atan2}(\pm \sqrt{1 - \text{C}^2\theta_i},\, \text{C}\theta_i) \quad & \text{si} \quad X = 0 \text{ et } Y \ne 0 \\ \text{atan2}(\text{S}\theta_i, \, \pm \sqrt{1 - \text{S}^2\theta_i}) \quad & \text{si} \quad X \ne 0 \text{ et } Y = 0 \\ \begin{cases} \theta_{i1} = \text{atan2}(-Y,X) \\ \theta_{i2} = \theta_{i1} + 180\deg \end{cases} \quad & \text{si} \quad X, \, Y \ne 0 \text{ et } Z = 0 \\ \text{atan2}(\text{S}\theta_i, \, \text{C}\theta_i) \quad & \text{si} \quad X, \, Y, \text{ et } Z \ne 0 \\ & \quad \, \, \, \, \text{ et } X^2+Y^2 \geq Z^2 \\ \text{configuration singulière} \quad & \text{si} \quad X, \, Y \ne 0 \\ \end{cases} \end{align*} \end{split}\]

Dans le cas où \(X \ne 0\) et \(Y \ne 0\) et \(Z \ne 0\), l’équation est résolue en élevant l’expression au carré : en remplaçant les termes en sinus par les fonctions équivalentes en cosinus, on aboutit à une équation du second degré à résoudre donnant la valeur du cosinus. Un raisonnement analogue est mené pour déterminer le terme en sinus :

\[\begin{split} \begin{equation*} \begin{cases} \text{C}\theta_i = \dfrac{YZ - \varepsilon X \sqrt{X^2+Y^2-Z^2}}{X^2 + Y^2} \\ \text{S}\theta_i = \dfrac{XZ + \varepsilon Y \sqrt{X^2+Y^2-Z^2}}{X^2 + Y^2} \\ \end{cases} \qquad \text{avec} \qquad \varepsilon = \pm 1 \end{equation*} \end{split}\]

Dans ce cas, la résolution de l’équation donne deux solutions, correspondant aux valeurs de \(\varepsilon\).

Solutions de l’équation de type 6 :

\[\begin{split} \begin{equation*} \begin{cases} W\text{S}\theta_j = X\text{C}\theta_i + Y \text{S}\theta_i + Z_1 \\ W\text{C}\theta_j = X\text{S}\theta_i - Y \text{C}\theta_i + Z_2 \\ \end{cases} \end{equation*} \end{split}\]

Solution : Elle consiste à élever au carré chaque équation pour faire disparaître \(\theta_j\) en les additionnant. \(\theta_i\) est alors résolu par une équation de type 2. Ensuite, connaissant \(\theta_i\), \(\theta_j\) est déterminé par un système d’équations de type 3.

Solutions de l’équation de type 3 :

\[\begin{split} \begin{equation*} \begin{cases} X_1\text{s}\theta_i + Y_1 \text{c}\theta_i = Z_1 \\ X_2\text{S}\theta_i + Y_2 \text{C}\theta_i = Z_2 \\ \end{cases} \end{equation*} \end{split}\]

Dans le cas où \(X_1 Y_2 - X_2 Y_1 \neq 0\), les termes en cosinus et sinus sont obtenus par combinaison linaire des deux équations pour éliminer respectivement les termes sinus et cosinus :

\[\begin{split} \begin{equation*} \begin{cases} \text{C}\theta_i = \dfrac{Z_2 X_1 - Z_1 X_2}{X_1 Y_2 - X_2 Y_1} \\ \text{S}\theta_i = \dfrac{Z_1 Y_2 - Z_2 Y_1}{X_1 Y_2 - X_2 Y_1} \\ \end{cases} \end{equation*} \end{split}\]

Dans le cas où \(X_1 Y_2 - X_2 Y_1 = 0\) alors, les équations ne sont plus indépendantes ; on choisit alors l’une des deux équations que l’on résout en équation de type 2. Solution :

\[\begin{split} \begin{align*} \theta_i = \begin{cases} \text{atan2}(\text{S}\theta_i, \, \text{C}\theta_i) \quad & \text{si} X_1 Y_2 - X_2 Y_1 \neq 0 \\\text{atan2}(\dfrac{Z_1}{X_1} \, \dfrac{Z_2}{Y_2} ) \quad & \text{si} Y_1 = 0 \text{ et } X_2 = 0 \\ \end{cases} \end{align*} \end{split}\]

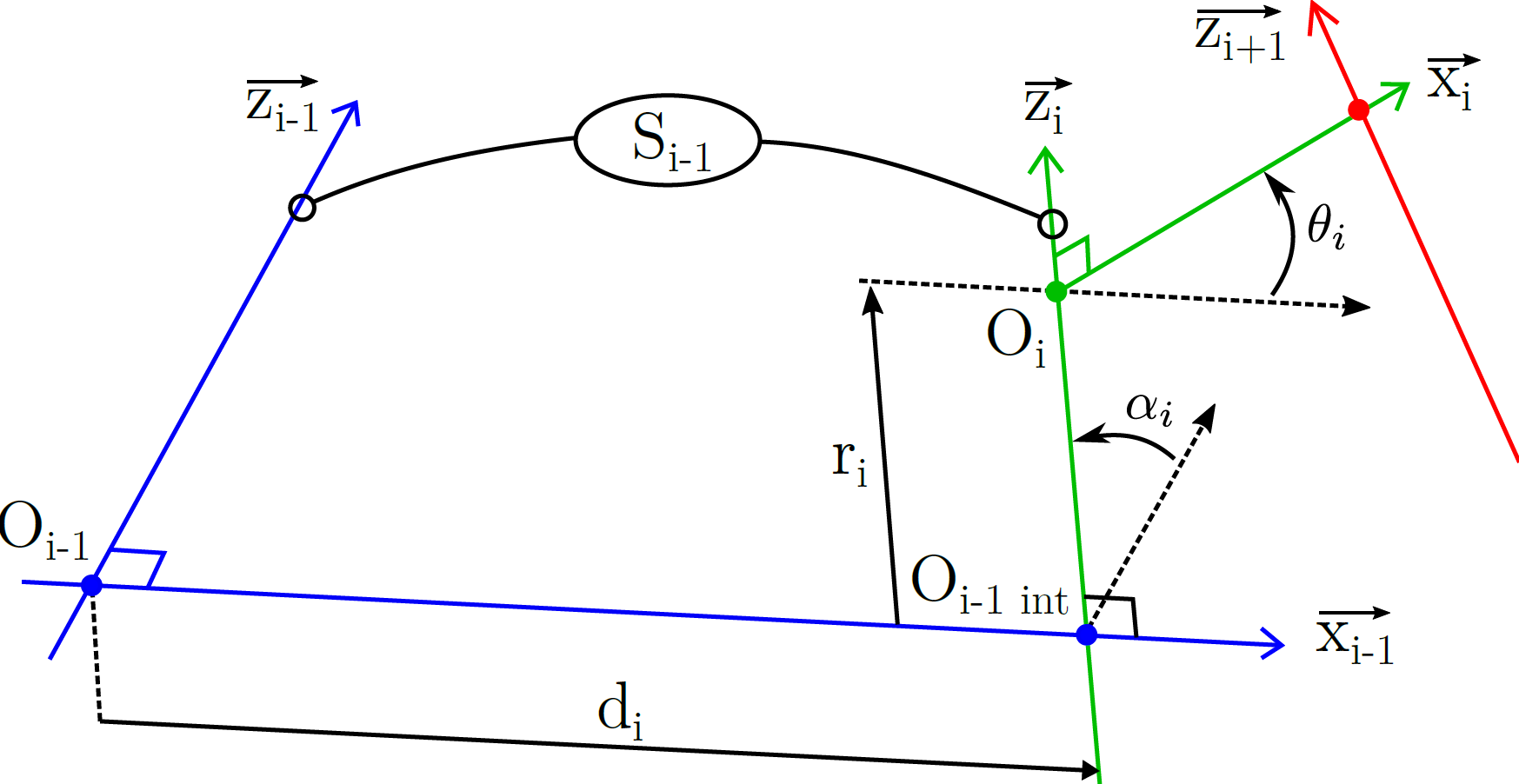
Fig. 78 Paramétrage de DHm

Document Réponse A

Il est demandé de représenter les axes \(x_i\) et \(z_i\) ainsi que les points \(O_i\). Concernant le paramétrage, les longueurs \(r_i\) et \(d_i\) devront être affichées ainsi que les angles \(\theta_i\) lorsqu’ils sont non nuls. Vous disposez d’une seconde figure au dos, au cas ou vous faites une erreur et que la figure n’est plus lisible. Si la seconde figure est utilisée, merci de préciser laquelle est la figure répondant à la Question 1.1.