Modèle cinématique

Introduction

La modélisation des positions des différents segments d’une structure articulée est un problème purement géométrique. Elle ne permet pas de décrire directement les variations de la géométrie de façon continue. Pour cela, on peut utiliser la dérivée du modèle géométrique : le modèle cinématique. Ce modèle, basé sur la matrice jacobienne, permet de mener de nombreuses méthodes et analyses :

• le calcul de la solution locale des variables articulaires \(\mathbf{q}\) à partir des coordonnées opérationnelles \(\mathbf{X}\);

• le calcul des singularités ;

• le calcul des dimensions de l’espace opérationnel accessible du robot ;

• l’étude statique reliant les efforts exercés par l’organe terminal sur l’environnement aux forces et couples des actionneurs… .

Matrice Jacobienne

Soit \(f_1\) une fonction permettant, à partir de données articulaires \(q_i\) d’exprimer une composante de l’espace des tâches :

\[ \begin{equation} x_1 = f_1(q_i, \xi) \end{equation} \]

Écriture de la différentielle :

\[ \begin{equation} dx_1 = \frac{\partial f_1}{\partial q_1}dq_1 + \frac{\partial f_1}{\partial q_2}dq_2+ \cdots + \frac{\partial f_1}{\partial q_n}dq_n \end{equation} \]

En écrivant les différentielles de chaque composante de l’espace des tâches, on arrive à :

(14)\[\begin{split} \begin{equation} \mathbf{dX} = \mathbf{J}(\mathbf{q})\mathbf{dq} \quad \text{avec} \quad \mathbf{J}(\mathbf{q}) = \begin{bmatrix} \frac{\partial f_1}{\partial q_1} & \frac{\partial f_1}{\partial q_2} & \cdots & \frac{\partial f_1}{\partial q_n} \\ \frac{\partial f_2}{\partial q_1} & \frac{\partial f_2}{\partial q_2} & \cdots & \frac{\partial f_2}{\partial q_n} \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_r}{\partial q_1} & \frac{\partial f_r}{\partial q_2} & \cdots & \frac{\partial f_r}{\partial q_n} \\ \end{bmatrix} \end{equation} \end{split}\]

où \(\mathbf{J}(\mathbf{q})\) est matrice jacobienne de dimensions \(m\times n\). Dans cette écriture, les coordonnées opérationnelles (ou configuration du repère \(\mathcal{R}_n\) par rapport à \(\mathcal{R}_0\)) sont décrite par le vecteur :

\[\begin{split} \begin{equation} \mathbf{X} = \begin{bmatrix} \mathbf{X}_r \\ \mathbf{X}_p \end{bmatrix} \end{equation} \end{split}\]

où les éléments \(\mathbf{X}_r\) et \(\mathbf{X}_p\) désignent respectivement l’orientation et la position.

Modèle différentiel

Il permet de faire le lien entre les variations de coordonnées de l’effecteur \(\Delta x\) et les variations articulaires correspondantes \(\Delta q\) :

\[ \begin{equation} \Delta x = \mathbf{J} \Delta q \end{equation} \]

Remarques

• un des avantages est d’avoir une expression des défauts \(\Delta x\) linéaire par rapport aux \(\Delta q\),

• le modèle différentiel présente un caractère local, car la valeur des différentielles \(\frac{\partial f}{\partial q}\) dépend de la configuration de la structure donc des \(q_i\),

• le modèle différentiel inverse peut être noté

  \[ \begin{equation} \Delta q = \mathbf{J}^{-1} \Delta x \end{equation} \]

  cependant, le calcul de \(\mathbf{J}^{-1}\) n’a pas toujours de solution ou pas de solutions en nombre fini.

  Le calcul de \(\mathbf{J}^{-1}\) impose que la matrice soit carrée, c’est-à-dire que le nombre d’axes \(n\) soit égal au nombre de d.d.l. de l’effecteur \(p\) et que le rang de \(\mathbf{J}\) soit \(n\). Il faut noter que le rang de \(\mathbf{J}\) peut dépendre de la configuration articulaire du robot, et peut diminuer localement.

Modèle cinématique

Définition

Le modèle cinématique décrit les vitesses de l’organe terminal en fonction des vitesses articulaires :

(15)\[ \begin{equation} \mathbf{\dot{X}} = \mathbf{J}(\mathbf{q}) \mathbf{\dot{q}} \end{equation} \]

Calcul du modèle cinématique

Par dérivation

Dans le cas des robots simples, souvent jusqu’à trois d.d.l., il est facile de calculer la matrice jacobienne \(\mathbf{J}(\mathbf{q})\) par dérivation du modèle géométrique direct (i.e. par dérivation au sens de la définition équation (14)).

Par calcul du jacobien de base

Pour des robots à plus de trois d.d.l., la matrice jacobienne \(\mathbf{J}(\mathbf{q})\) peut être déterminée par le calcul direct (méthodes de calcul cinématiques usuelles de la mécanique du solide) des expressions reliant les vitesses et vecteurs rotations de chaque repère en fonction de la géométrie et des paramètres articulaires.

Pour cela, on exprime d’abord ces relations indépendamment du paramétrage choisi (i.e. cosinus directeurs, Euler ou Briant, intrinsèque - extrinsèque). Cette formulation est nommée « jacobien de base » \(\mathbf{J}_n\). Sous forme différentielle, l’expression correspond à :

(16)\[\begin{split} \begin{equation} \begin{bmatrix} \delta_n \\ \mathbf{d}_n \end{bmatrix} = \mathbf{J}_n\mathbf{dq} \end{equation} \end{split}\]

où \(\mathbf{d}_n\) représente le vecteur de translation différentiel et \(\delta_n\) le vecteur de rotation différentielle. Sous forme cinématique, l’expression correspond à :

(17)\[\begin{split} \begin{equation} \begin{bmatrix} \omega_n \\ \mathbf{V}_n \end{bmatrix} = \mathbf{J}_n \mathbf{\dot{q}} \end{equation} \end{split}\]

où \(\mathbf{V}_n\) et \(\omega_n\) sont les deux éléments du réduction du torseur cinématique du repère \(\mathcal{R}_n\) dans son mouvement par rapport au référentiel de base \(\mathcal{R}_0\). Une fois le jacobien de base formulé, il est possible de remonter aux coordonnées opérationnelles par la formulation :

\[\begin{split} \begin{align} \mathbf{\dot{X}} &= \mathbf{J}(\mathbf{q}) \mathbf{\dot{q}} \nonumber \\ &= \mathbf{\Omega}\ \mathbf{J}_n \ ^0 \mathbf{\dot{q}} \\ \end{align} \end{split}\]

La matrice \(\mathbf{\Omega}\) permet convertir les expressions cartésiennes des vitesses en fonction du paramétrage choisi pour l’orientation. Elle permet donc de remonter aux coordonnées opérationnelles.

\[\begin{split} \begin{equation} \begin{bmatrix} \mathbf{\dot{X}}_r \\ \mathbf{\dot{X}}_p \\ \end{bmatrix} = \begin{bmatrix} \mathbf{\Omega}_r & \mathbf{0}_3 \\ \mathbf{0}_3 & \mathbf{\Omega}_p \end{bmatrix}= \begin{bmatrix} ^0\omega_n \\ ^0\mathbf{V}_n \end{bmatrix} \end{equation} \end{split}\]

Expression du jacobien de base \(\mathbf{J}_n\)

Le calcul de \(\mathbf{J}_n\) peut être facilement effectué en utilisant les relations de composition de mouvement ; cette méthode est donc naturellement particulièrement adaptée aux architectures simples ouvertes.

Composition des vecteurs rotations :

\[\begin{split} \begin{align} \omega_n &= \omega_{\mathcal{B}_n / \mathcal{B}_0} \nonumber \\ & =\omega_{\mathcal{B}_n / \mathcal{B}_{n-1}} + \omega_{\mathcal{B}_{n-1} / \mathcal{B}_{n-2}} + \cdots + \omega_{\mathcal{B}_1 / \mathcal{B}_{0}} \nonumber \\ & = \sum^n_{k=1} \omega_{\mathcal{B}_k / \mathcal{B}_{k-1}} \nonumber \\ & = \sum^n_{k=1} \omega_{k} \end{align} \end{split}\]

Composition des vecteurs vitesses :

\[\begin{split} \begin{align} \mathbf{V}_n &= \mathbf{V}_{O_n \in \mathcal{R}_n / \mathcal{R}_0} \nonumber \\ &= \mathbf{V}_{O_n \in \mathcal{R}_n / \mathcal{R}_{n-1}} + \mathbf{V}_{O_n \in \mathcal{R}_{n-1} / \mathcal{R}_{n-2}} + \cdots + \mathbf{V}_{O_n \in \mathcal{R}_1 / \mathcal{R}_0} \nonumber \\ & = \sum^n_{k=1} \mathbf{V}_{O_n \in \mathcal{R}_k / \mathcal{R}_{k-1}} \nonumber \\ & = \sum^n_{k=1} ( \mathbf{V}_{O_k \in \mathcal{R}_k / \mathcal{R}_{k-1}} + \mathbf{L}_{k,n} \wedge \omega_k ) \quad \text{avec} \quad \mathbf{L}_{k,n} = \mathbf{O}_n \mathbf{O}_k \nonumber \\ & = \sum^n_{k=1} \mathbf{V}_{k,n} \end{align} \end{split}\]

où le vecteur vitesse \(\mathbf{V}_{k,n}\) représente la contribution de la liaison \(k\) à la vitesse du repère \(\mathcal{R}_n\) par rapport au repère \(\mathcal{R}_0\).

Suivant la nature de la k-ième liaison considérée, les expressions se réduisent :

• pour les liaisons pivots :

  \[\begin{split} \begin{align} \omega_k &= \dot{q_k}\mathbf{z}_k \\ \mathbf{V}_{k,n}&= \mathbf{L}_{k,n}\wedge \dot{q_k}\mathbf{z}_k \end{align} \end{split}\]

  avec selon le paramétrage de Denavit et Hartenberg modifié \(\dot{q_k} = \dot{\theta_k}\).

• pour les liaisons glissières :

  \[\begin{split} \begin{align} \omega_k &= \mathbf{0} \\ \mathbf{V}_{k,n}&= \dot{q_k}\mathbf{z}_k \end{align} \end{split}\]

  avec selon le paramétrage de Denavit et Hartenberg modifié \(\dot{q_k} = \dot{r_k}\).

Par identification des deux expressions précédentes avec l’équation (17), le jacobien de base prend alors une expression de la forme :

\[ \begin{equation} \mathbf{J}_n = \left[ \mathbf{J}_{n,1}, \cdots, \mathbf{J}_{n,k}, \cdots, \mathbf{J}_{n,n}\right] \end{equation} \]

avec :

• pour les liaisons pivots :

\[\begin{split} \begin{equation} \mathbf{J}_{n,k} = \begin{bmatrix} \mathbf{z}_k \\ \mathbf{L}_{k,n}\wedge \mathbf{z}_k \end{bmatrix} \end{equation} \end{split}\]

• pour les liaisons glissières :

\[\begin{split} \begin{equation} \mathbf{J}_{n,k} = \begin{bmatrix} \mathbf{0} \\ \mathbf{z}_k \end{bmatrix} \end{equation} \end{split}\]

Expression de la matrice \(\Omega\) selon le paramétrage en orientation

Expression générale de la matrice \(\Omega\)

La matrice \(\mathbf{\Omega}_p\) permet de faire le lien entre la vitesse linéaire \(\mathbf{V}_n\) du repère \(\mathcal{R}_n\) et la vitesse linéaire \(\mathbf{\dot{X}}_p\) des coordonnées opérationnelles :

\[ \begin{equation} \mathbf{\dot{X}}_p = \mathbf{\Omega}_p \ ^0 \mathbf{V}_n \end{equation} \]

La plupart du temps, le jacobien de base global \(\mathbf{J}_n\) est exprimé dans le repère de base \(\mathcal{R}_0\), soit \(^0\mathbf{J}_n\). \(\mathbf{\Omega}_p\) se réduit donc à la matrice identité.

(18)\[ \begin{equation} \mathbf{\Omega}_p = \mathbf{I}_3 \end{equation} \]

La matrice r dépend du paramétrage choisi pour repérer l’orientation de Bn par rapport à B0

\[ \begin{equation} \mathbf{\dot{X}}_r = \mathbf{\Omega}_r \ ^0 \omega_n \end{equation} \]

Étant donné la remarque de l’équation (18), la formulation de la matrice globale devient :

\[\begin{split} \begin{equation} \mathbf{\Omega} = \begin{bmatrix} \mathbf{\Omega}_r & \mathbf{0}_3 \\ \mathbf{0}_3 & \mathbf{I}_3 \\ \end{bmatrix} \end{equation} \end{split}\]

et donc les formulations de la matrice inverse pour les paramétrages d’Euler et Bryan :

\[\begin{split} \begin{equation} \mathbf{\Omega}^{-1} = \begin{bmatrix} \mathbf{\Omega}_r^{-1} & \mathbf{0}_3 \\ \mathbf{0}_3 & \mathbf{I}_3 \\ \end{bmatrix} \end{equation} \end{split}\]

et de la matrice pseudo-inverse (multiplication à gauche, matrice non carrée) pour les paramétrages par les cosinus directeurs et les quaternions :

\[\begin{split} \begin{equation} \mathbf{\Omega}^{\dagger} = \begin{bmatrix} \mathbf{\Omega}_r^{\dagger} & \mathbf{0}_3 \\ \mathbf{0}_3 & \mathbf{I}_3 \\ \end{bmatrix} \end{equation} \end{split}\]

avec

\[\begin{split} \begin{equation} \begin{cases} \mathbf{\Omega}^{\dagger} = (\mathbf{\Omega}^t \mathbf{\Omega})^{-1} \mathbf{\Omega}^t \\ \mathbf{\Omega}^{\dagger} \mathbf{\Omega} = \mathbf{I}_3 \end{cases} \end{equation} \end{split}\]

Expression de \(\Omega_r\) pour un paramétrage par les cosinus directeurs

Les dérivées des trois vecteurs élémentaires définissant la base \(\mathcal{B}_n\) par rapport au temps dans la base \(\mathcal{B}_0\) s’écrivent :

(19)\[ \begin{equation} ^0 \mathbf{\dot{x}}_n = \frac{d\ ^0 \mathbf{\dot{x}}_n}{dt}_{\vert \mathcal{B}_0} = \ ^0\omega_n \wedge \ ^0\mathbf{\dot{x}}_n \end{equation} \]

\[ \begin{equation} ^0 \mathbf{\dot{y}}_n = \frac{d\ ^0\mathbf{\dot{y}}_n}{dt}_{\vert \mathcal{B}_0} = \ ^0\omega_n \wedge \ ^0\mathbf{\dot{y}}_n \end{equation} \]

(20)\[ \begin{equation} ^0 \mathbf{\dot{z}}_n = \frac{d\ ^0\mathbf{\dot{z}}_n}{dt}_{\vert \mathcal{B}_0} = \ ^0\omega_n \wedge \ ^0\mathbf{\dot{z}}_n \end{equation} \]

En utilisant la matrice de pré-produit vectoriel, et en appliquant la formulation précédente pour chaque vecteur élémentaire de la base \(\mathcal{B}_n\), on écrit :

\[\begin{split} \begin{equation} \mathbf{\dot{X}}_r = \begin{bmatrix} ^0\mathbf{\dot{x}}_n \\ ^0\mathbf{\dot{y}}_n \\ ^0\mathbf{\dot{z}}_n \end{bmatrix} = \begin{bmatrix} - ^0\mathbf{\hat{x}}_n \\ - ^0\mathbf{\hat{y}}_n \\ - ^0\mathbf{\hat{z}}_n \end{bmatrix} \ ^0\omega_n = \mathbf{\Omega}_r \ ^0\omega_n \end{equation} \end{split}\]

Dans ce cas, \(\mathbf{\Omega}_r\) est une matrice \(9 \times 3\) ; vu que la matrice de pré-produit vectoriel est antisymétrique, nous pouvons écrire :

\[\begin{split} \begin{align} \mathbf{\Omega}_r^t \mathbf{\Omega}_r &= \begin{bmatrix} ^0 \mathbf{\hat{x}}_n & ^0 \mathbf{\hat{y}}_n & ^0\mathbf{\hat{z}}_n \end{bmatrix} \begin{bmatrix} - ^0\mathbf{\hat{x}}_n \\ - ^0\mathbf{\hat{y}}_n \\ - ^0\mathbf{\hat{z}}_n \end{bmatrix} \\ &= 2\ \mathbf{I}_3 \end{align} \end{split}\]

A partir de cette équation on obtient la pseudo inverse \(\mathbf{\Omega}_r^{\dagger}\) par :

\[\begin{split} \begin{align} \mathbf{\Omega}_r^{dag} &= (\mathbf{\Omega}_r^t\mathbf{\Omega}_r)^{-1} \mathbf{\Omega}_r^t \\ &= \frac{1}{2}\mathbf{I}_3\mathbf{\Omega}_r^t \\ &= \frac{1}{2}\begin{bmatrix} ^0 \mathbf{\hat{x}}_n & ^0 \mathbf{\hat{y}}_n & ^0\mathbf{\hat{z}}_n \end{bmatrix} \end{align} \end{split}\]

Expression de \(\Omega_r\) pour un paramétrage par les angles d’Euler

Le paragraphe 2.2.2 définit le paramétrage d’Euler. En traduisant, d’un point de vue cinématique, les rotations successives autour de vecteurs projetés dans la base de référence \(\mathcal{B}_0\), le vecteur rotation de \(\mathcal{B}_0\) par rapport à \(\mathcal{B}_n\) s’écrit :

\[\begin{split} \begin{align} ^0\omega_n &= \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \dot{\phi} + \begin{bmatrix} \text{C}\phi \\ \text{S}\phi \\ 0 \end{bmatrix} \dot{\theta} + \begin{bmatrix} \text{S}\phi \text{C}\theta \\ -\text{C}\phi \text{S}\theta \\ \text{C}\theta \end{bmatrix} \dot{\psi} \\ &= \begin{bmatrix} 0 & \text{C}\phi & \text{S}\phi \text{C}\theta \\ 0 & \text{s}\phi & - \text{C}\phi \text{S}\theta\\ 1 & 0 & \text{C}\theta \end{bmatrix} \begin{bmatrix} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{bmatrix} \\ &=\mathbf{\Omega}^{-1} \dot{\mathbf{X}}_r \end{align} \end{split}\]

ce qui permet par identification d’en déduire les matrices directe et inverse :

\[\begin{split} \begin{equation} \mathbf{\Omega}_r = \begin{bmatrix} -\text{S}\phi \text{cotg} \theta & \text{C}\phi \text{cotg} \theta & 1 \\ \text{C}\phi & \text{S}\phi & 0 \\ \text{S}\phi / \text{S} \theta & \text{C}\phi / \text{S} \theta & 0 \end{bmatrix} \end{equation} \end{split}\]

Dans cette expression on retrouve la singularité de représentation par les angles d’Euler (pour \(\theta = 0\) ou \(\pi\)), comme vu au paragraphe 2.2.2.

Expression de \(\Omega_r\) pour un paramétrage par les angles de Bryan

Le même raisonnement que précédemment appliqué au paramétrage de Bryan, défini au paragraphe 2.2.3, aboutit à :

\[\begin{split} \begin{align} ^0\omega_n &= \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \dot{\phi} + \begin{bmatrix} -\text{S}\phi \\ \text{C}\phi \\ 0 \end{bmatrix} \dot{\theta} + \begin{bmatrix} \text{C}\phi \text{C}\theta \\ \text{S}\phi \text{C}\theta \\ -\text{S}\theta \end{bmatrix} \dot{\psi} \\ &= \begin{bmatrix} 0 & - \text{S}\phi & \text{C}\phi \text{C}\theta \\ 0 & \text{C}\phi & - \text{S}\phi \text{C}\theta\\ 1 & 0 & -\text{S}\theta \end{bmatrix} \begin{bmatrix} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{bmatrix} \\ &=\mathbf{\Omega}^{-1} \dot{\mathbf{X}}_r \end{align} \end{split}\]

et la matrice directe :

\[\begin{split} \begin{equation} \mathbf{\Omega}_r = \begin{bmatrix} \text{C}\phi \text{tan} \theta & \text{S}\phi \text{tan} \theta & 1 \\ -\text{S}\phi & \text{C}\phi & 0 \\ \text{C}\phi / \text{C} \theta & \text{S}\phi / \text{C} \theta & 0 \end{bmatrix} \end{equation} \end{split}\]

qui fait réapparaître la singularité de représentation par les angles de Bryan (pour \(\theta = \pm \frac{\pi}{2}\)).

Expression de \(\Omega_r\) pour un paramétrage par les quaternions

En dérivant la matrice (8) par rapport au temps, et en utilisant les formulations (19) à (20) on peut écrire :

\[\begin{split} \begin{align} \frac{d\ \mathbf{R}_{0n}}{dt}_{\vert \mathcal{B}_0} &= \begin{bmatrix} ^0 \mathbf{\dot{x}}_n & ^0 \mathbf{\dot{y}}_n & ^0\mathbf{\dot{z}}_n \end{bmatrix} \nonumber \\ &= \begin{bmatrix} ^0\omega_n \wedge \ ^0 \mathbf{x}_n & ^0\omega_n \wedge \ ^0 \mathbf{y}_n & ^0\omega_n \wedge \ ^0\mathbf{z}_n \end{bmatrix} \end{align} \end{split}\]

Sur cette égalité de matrices, l’identification des termes diagonaux mène au système de trois équations :

(21)\[\begin{split} \begin{equation} \begin{cases} 2(Q_1\dot{Q}_1+Q_2\dot{Q}_2)=(Q_2Q_4-Q_1Q_3)\ ^0\omega_n \cdot \mathbf{y}_0 -(Q_2Q_3+Q_1Q_4)\ ^0\omega_n \cdot \mathbf{z}_0 \\ 2(Q_1\dot{Q}_1+Q_3\dot{Q}_3)=(Q_2Q_3+Q_1Q_4)\ ^0\omega_n \cdot \mathbf{z}_0 -(Q_3Q_4+Q_1Q_2)\ ^0\omega_n \cdot \mathbf{x}_0 \\ 2(Q_1\dot{Q}_1+Q_4\dot{Q}_4)=(Q_3Q_4+Q_1Q_2)\ ^0\omega_n \cdot \mathbf{x}_0 -(Q_2Q_4+Q_1Q_3)\ ^0\omega_n \cdot \mathbf{y}_0 \end{cases} \end{equation} \end{split}\]

La dérivation de l’équation (7) aboutit à :

\[ \begin{equation} Q_1\dot{Q}_1+Q_2\dot{Q}_2 +Q_3\dot{Q}_3+Q_4\dot{Q}_4 =0 \end{equation} \]

Ce qui permet, avec le système d’équations (21) d’aboutir à :

\[\begin{split} \begin{equation} \mathbf{\dot{X}}_r = \mathbf{\dot{Q}} = \begin{bmatrix} \dot{Q}_1 \\ \dot{Q}_2 \\ \dot{Q}_3 \\ \dot{Q}_4 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} -Q_2 & -Q_3 & -Q_4 \\ Q_1 & Q_4 & - Q_3 \\ -Q_4 & Q_1 & Q_2 \\ Q_3 & - Q_2 & Q_1 \end{bmatrix} \ ^0\omega_n \end{equation} \end{split}\]

d’où :

\[\begin{split} \begin{equation} \mathbf{\Omega}_r = \begin{bmatrix} -Q_2 & -Q_3 & -Q_4 \\ Q_1 & Q_4 & - Q_3 \\ -Q_4 & Q_1 & Q_2 \\ Q_3 & - Q_2 & Q_1 \end{bmatrix} \end{equation} \end{split}\]

Enfin, en remarquant que :

\[ \begin{equation} \mathbf{\Omega}_r^t \mathbf{\Omega}_r = \frac{1}{4}\mathbf{I}_4 \end{equation} \]

On trouve la matrice pseudo-inverse :

\[\begin{split} \begin{align} \mathbf{\Omega}_r^{\dagger} &= (\mathbf{\Omega}_r^t\mathbf{\Omega}_r)^{-1} \mathbf{\Omega}_r^t \\ &= 4 \mathbf{\Omega}_r^t \end{align} \end{split}\]

Modèle cinématique du second ordre

Il permet de calculer les accélérations de l’espace des tâches en fonction des positions, vitesses et accélérations des paramètres articulaires. Par dérivation du modèle cinématique (équation (15)) :

\[ \begin{equation} \mathbf{\ddot{X}} = \mathbf{J}(\mathbf{q}) \mathbf{\ddot{q}} + \mathbf{\dot{J}}(\mathbf{q},\mathbf{\dot{q}})\mathbf{\dot{q}} \quad \text{avec} \quad \mathbf{\dot{J}}(\mathbf{q},\mathbf{\dot{q}}) = \frac{d}{dt}\mathbf{J}(\mathbf{q}) \end{equation} \]

Singularité

Soit m le nombre de degrés de liberté (d.d.l.) de l’espace opérationnel donné par le robot. Dans le cas classique des structures 6 axes, il vaut 6 et correspond aux 3 translations et 3 rotations de l’espace qu’il est possible de faire faire à l’effecteur par rapport à un référentiel de base.

Pour une configuration donnée \(\mathbf{q}\), on nomme \(r\) le rang de la matrice jacobienne \(\mathbf{J}\) :

\[ \begin{equation} r = \text{rg}(\mathbf{J}(\mathbf{q})) \end{equation} \]

En fonction de la configuration \(\mathbf{q}\), \(r\) peut diminuer : \(r < m\); on parle alors de singularité d’ordre \(m-r\).

Soit \(n\) le nombre de degrés de liberté du robot (nombre d’articulations).

• Si \(m = n\) le robot est non redondant. Il dispose du nombre juste de liaisons permettant de donner le nombre m de d.d.l. à l’organe terminal.

• Si \(m < n\) le robot est redondant d’ordre \(n-m\). Il dispose de plus d’articulations qu’il n’en faut pour donner le nombre \(m\) de d.d.l. à l’organe terminal.

Pour un robot 6 axes classique, la matrice \(\mathbf{J}\) est carrée, les singularités sont présentes en chaque configuration \(\mathbf{q}\) telles que :

\[ \begin{equation} \exists \mathbf{q} \in \mathbb{R}^n, \text{det}(\mathbf{J}) = 0 \end{equation} \]

Pour un robot redondant, les singularités peuvent être déterminées par :

\[ \begin{equation} \exists \mathbf{q} \in \mathbb{R}^n, \text{det}(\mathbf{J}\mathbf{J}^t) = 0 \end{equation} \]

La Fig. 19 présente les deux singularités pour le robot 5R Denso VP5243. Il s’agit d’une singularité dite d” « épaule » (image de gauche) où les liaisons 1 et 5 sont coaxiales et de « coude » (image de droite) où les axes des liaisons 2, 3 et 4 sont coplanaires.

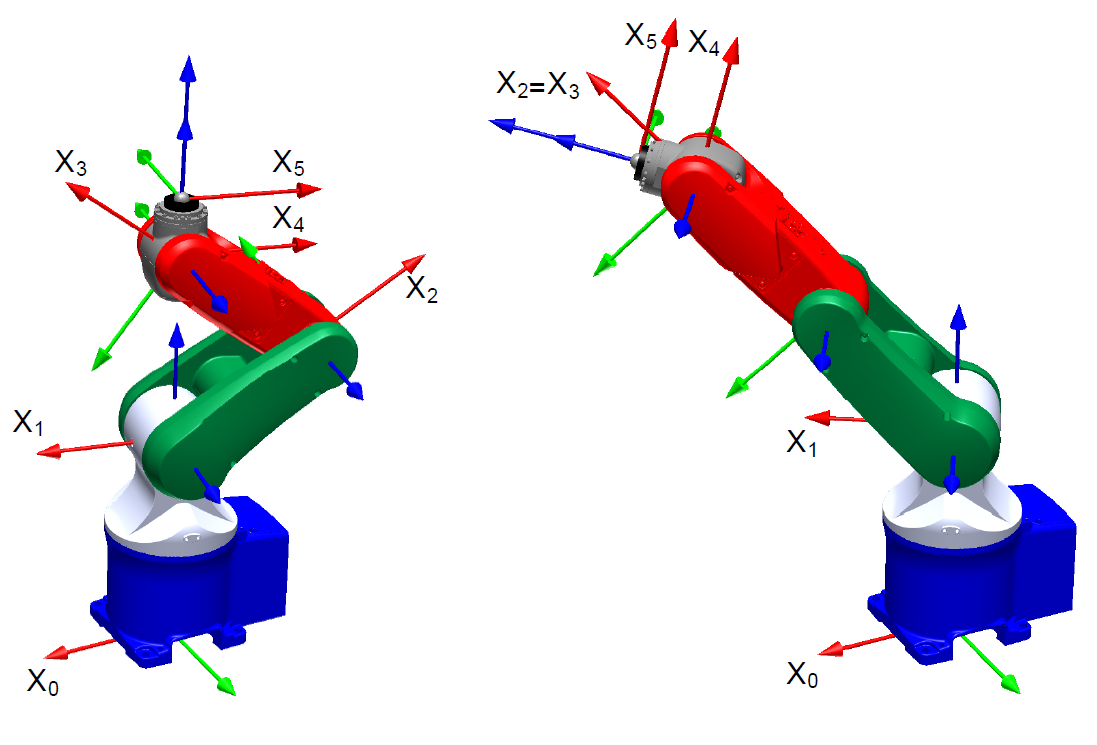
Fig. 19 Les deux singularités d’un robot 5 axes RRRRR