Éléments mathématiques

Base d’espace vectoriel

Soit un vecteur libre, désigné de façon intrinsèque (indépendamment de toute base) par son identificateur géométrique \( \overrightarrow{v} \) et son identificateur algébrique \(\mathbf{v}\). Pour déterminer sa valeur, il est nécessaire de le rapporter à une base d’espace vectoriel \(\mathcal{B}\) définie elle-même par \(n\) vecteurs unitaires (figure Fig. 1).

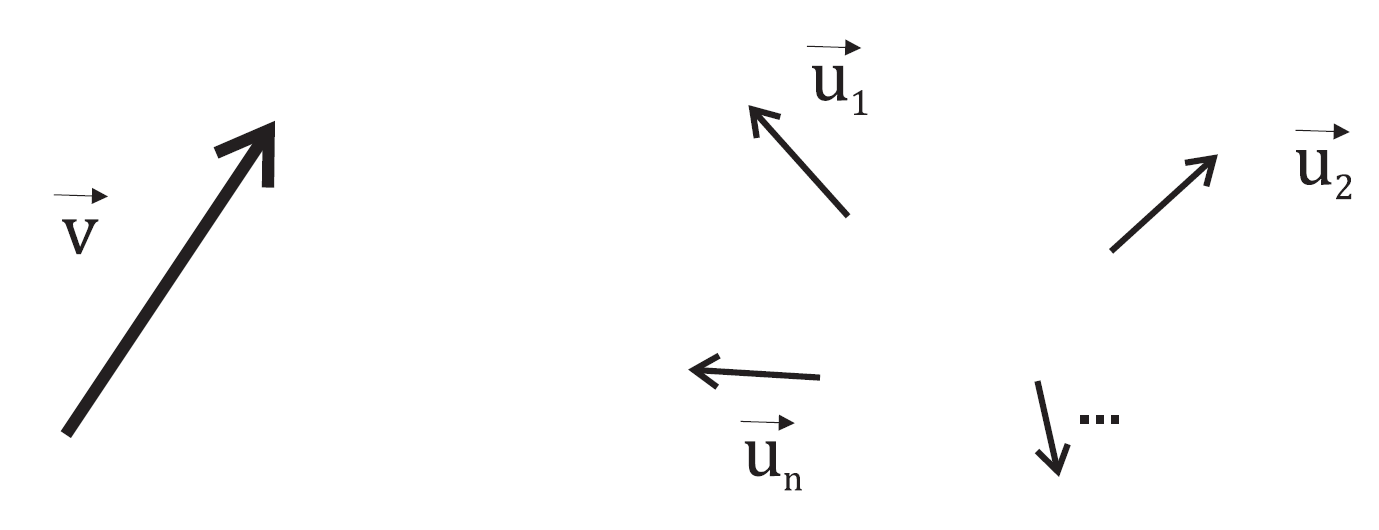
Fig. 1 Vecteur et base d’espace vectoriel

\[ \begin{equation} \mathcal{B} = (\mathbf{u_1},\mathbf{u_2}, \cdots, \mathbf{u_n}) \end{equation} \]

Les propriétés géométriques des vecteurs unitaires permettent de définir le vecteur \(\mathbf{v}\) comme la combinaison linéaire suivante :

\[ \begin{equation} \mathbf{v} = a_1\mathbf{u_1} + a_1\mathbf{u_1} + \cdots + a_n\mathbf{u_n} \end{equation} \]

Dans la base d’espace vectoriel \(\mathcal{B}\), le vecteur \(\mathbf{v}\) a pour coordonnées l’ensemble ordonné de \(n\) valeurs scalaires :

\[\begin{split} \begin{equation} \mathbf{v} = \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix}_{\mathcal{B}} \end{equation} \end{split}\]

Tout vecteur de norme finie se décrit donc de manière unique dans l’espace vectoriel considéré à \(n\) dimensions.

Changement de base d’expression

On cherche à expliciter dans une base \(\mathcal{B}_1\) un vecteur \(\mathbf{v}\) défini par ses coordonnées connues dans une base \(\mathcal{B}_2\) (figure Fig. 2). Les notations du vecteur dans les deux bases sont :

\[\begin{split} \begin{equation} \mathcal{B}_1 = (\mathbf{x_1}, \mathbf{y_1}, \mathbf{z_1}) \qquad \mathbf{v} =\ ^1\mathbf{v} = \begin{bmatrix} a_1 \\ b_1 \\ c_1 \end{bmatrix}_{\mathcal{B}_1} \end{equation} \end{split}\]

\[\begin{split} \begin{equation} \mathcal{B}_2 = (\mathbf{x_2}, \mathbf{y_2}, \mathbf{z_2}) \qquad \mathbf{v} =\ ^2\mathbf{v} = \begin{bmatrix} a_2 \\ b_2 \\ c_2 \end{bmatrix}_{\mathcal{B}_2} \end{equation} \end{split}\]

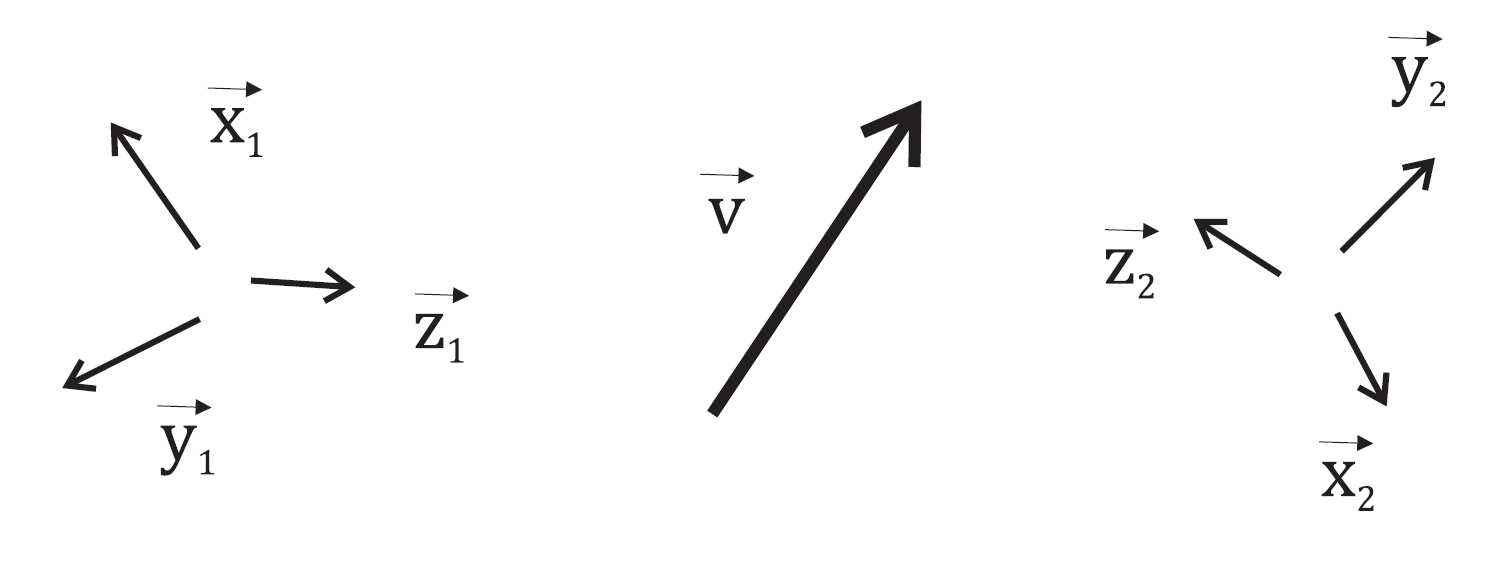
Fig. 2 Changement de bases

Matrice de changement de base d’expression

Pour exprimer les coordonnées de \(\mathbf{v}\) dans la base \(\mathcal{B}_1\), il est nécessaire de connaître l’expression des vecteurs unitaires de \(\mathcal{B}_2\) dans la base \(\mathcal{B}_1\). On définit ainsi \(\mathbf{R}_{12}\) comme étant la matrice de passage de la base \(\mathcal{B}_1\) à la base \(\mathcal{B}_2\) :

\[\begin{split} \begin{equation} \mathbf{R}_{12} = \begin{bmatrix} \mathbf{x_1} \cdot \mathbf{x_2} & \mathbf{x_1} \cdot \mathbf{y_2} & \mathbf{x_1} \cdot \mathbf{z_2} \\ \mathbf{y_1} \cdot \mathbf{x_2} & \mathbf{y_1} \cdot \mathbf{y_2} & \mathbf{y_1} \cdot \mathbf{z_2} \\ \mathbf{z_1} \cdot \mathbf{x_2} & \mathbf{z_1} \cdot \mathbf{y_2} & \mathbf{z_1} \cdot \mathbf{z_2} \\ \end{bmatrix} \end{equation} \end{split}\]

Exemple

\[\begin{split} \begin{equation*} \mathbf{R}_{12} = \begin{bmatrix} \text{C}\alpha & -\text{S}\alpha & 0 \\ \text{S}\alpha & \text{C}\alpha & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \end{equation*} \end{split}\]

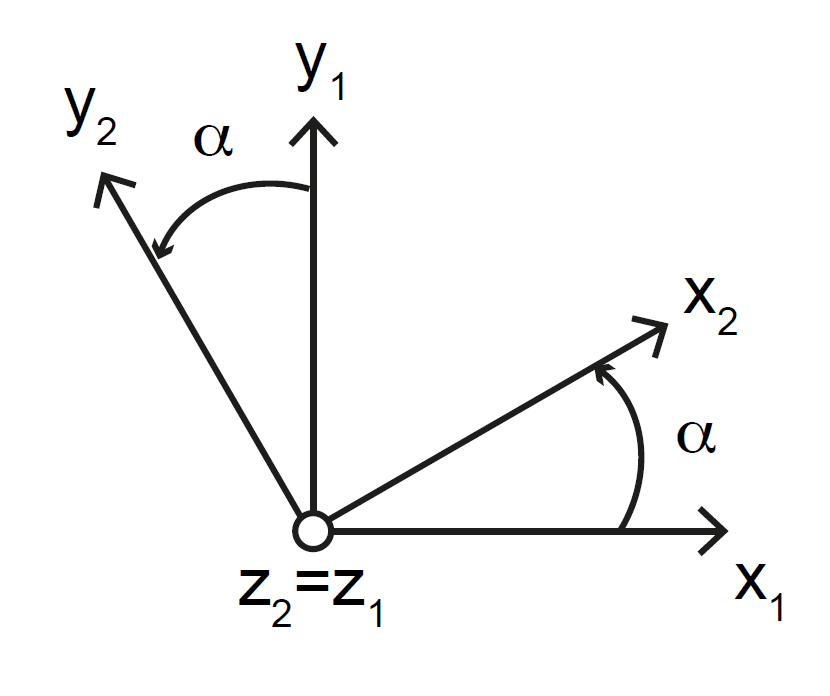
Fig. 3 Exemple de rotation \((\overrightarrow{z_1}, \alpha)\) entre les bases \(\mathcal{B}_1\) et \(\mathcal{B}_2\)

Les expressions de \(\mathbf{v}\) dans les bases \(\mathcal{B}_1\) et \(\mathcal{B}_2\) sont alors reliées par :

\[\begin{split} \begin{equation} ^1\mathbf{v} = \mathbf{R}_{12}\ ^2\mathbf{v} \qquad \Leftrightarrow \qquad \begin{bmatrix} a_1 \\ b_1 \\ c_1 \end{bmatrix}_{\mathcal{B}_1} = \mathbf{R}_{12} \begin{bmatrix} a_2 \\ b_2 \\ c_2 \end{bmatrix}_{\mathcal{B}_2} \end{equation} \end{split}\]

Pour un changement entre bases orthonormées, cet opérateur est orthogonal. Le changement d’expression inverse s’écrit :

\[ \begin{equation} \mathbf{R}_{21} = \mathbf{R}_{12}^t = \mathbf{R}_{12}^{-1} \end{equation} \]

Ainsi, on retrouve bien évidemment la relation :

\[ \begin{equation} \mathbf{R}_{12} \mathbf{R}_{21} = \mathbf{I}_d \end{equation} \]

Succession de changements de bases

Si on cumule différents changements de repères, la composition des projections s’exprime alors par multiplications des matrices de passage :

(1)\[\begin{split} \begin{align} ^1\mathbf{v} &= \mathbf{R}_{12} \mathbf{R}_{23} \cdots \mathbf{R}_{(n-1)n}\ ^n\mathbf{v} \\ &= \mathbf{R}_{1n}\ ^n\mathbf{v} \qquad \text{avec} \qquad \mathbf{R}_{1n} = \mathbf{R}_{12} \mathbf{R}_{23} \cdots \mathbf{R}_{(n-1)n} \end{align} \end{split}\]

Pour cette écriture, une multiplication à droite signifie qu’un changement de base supplémentaire est ajouté à la base courante (dernière base transformée) ; une multiplication à gauche signifie qu’un changement de base supplémentaire est ajouté à la base de départ.

Rotation de vecteur

Matrice de rotation

Soit un vecteur \(\mathbf{P}_1\) qui se retrouve pivoté vers le vecteur \(\mathbf{P}_2\) après une rotation. Si la rotation entre les vecteurs est définie par une rotation d’une base \(\mathcal{B}_1\) à une base \(\mathcal{B}_2\), le lien entre \(\mathbf{P}_1\) et \(\mathbf{P}_2\) est donné par :

\[ \begin{equation} \mathbf{P}_2 = \mathbf{R}_{12} \mathbf{P}_1 \end{equation} \]

Il faut bien noter que dans cette formulation, les deux vecteurs, ainsi que la transformation \(\mathbf{R}_{12}\) doivent être exprimés dans une même base, \(\mathcal{B}\) pour faire le calcul.

Exemple

\[\begin{split} \begin{equation*} \mathbf{R}_{12} = \begin{bmatrix} \text{C}\alpha & -\text{S}\alpha & 0 \\ \text{S}\alpha & \text{C}\alpha & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \end{equation*} \end{split}\]

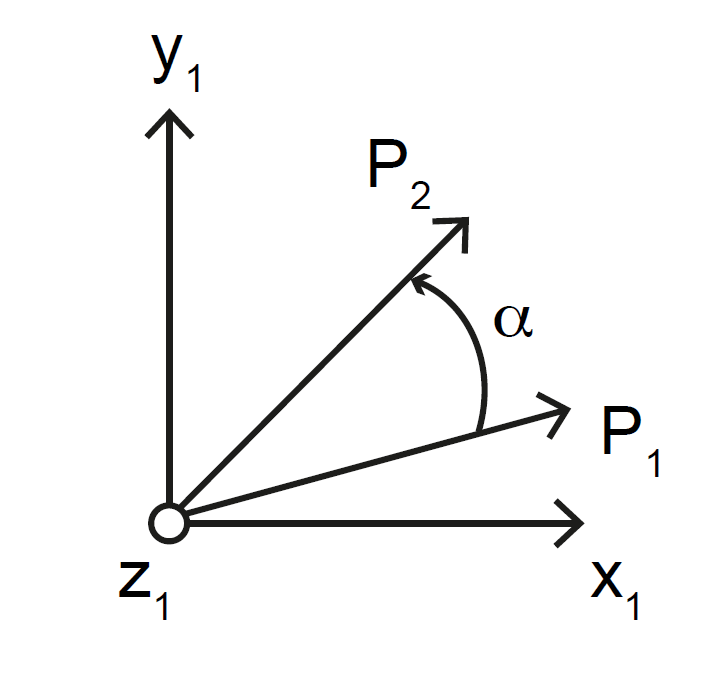
Fig. 4 Exemple de rotation \((\overrightarrow{z_1}, \alpha)\) du vecteur \(\mathbf{P}_1\) donnant le vecteur \(\mathbf{P}_2\)

Succession de rotations

On réalise maintenant une succession de rotations sur un point \(\mathbf{P}_1\). La composition des rotations s’exprime alors par la succession des multiplications des rotations élémentaires :

\[ \begin{equation} \mathbf{P}_n = \mathbf{R}_{(n-1)n} \cdots \mathbf{R}_{23} \mathbf{R}_{12}\ \mathbf{P}_1 \end{equation} \]

qui peut se réécrire sous la forme :

\[ \begin{equation} \mathbf{P}_1 = \mathbf{R}_{12}^{-1} \mathbf{R}_{23}^{-1} \cdots \mathbf{R}_{(n-1)n}^{-1} \mathbf{P}_n \end{equation} \]

Équivalence des opérations de rotation et de changement de base d’expression

Pour un changement de base, l’opérateur ne modifie pas la nature du vecteur (i.e. c’est toujours le même vecteur, il n’est pas transformé) par contre, les composantes sont fonction de la nouvelle base d’expression. L’opération de changement de base peut être vue comme une rotation, dite passive, de la base : rotation de la base initiale vers la nouvelle base d’expression. L’équation (1) peut alors s’écrire sous la forme suivante pour exprimer le lien entre les composantes dans les systèmes de coordonnées initial et tourné :

\[\begin{split} \begin{align} ^n\mathbf{v} &= \mathbf{R}_{n1} \ ^1\mathbf{v} \\ &= \left( \mathbf{R}_{12} \mathbf{R}_{23} \cdots \mathbf{R}_{(n-1)n} \right)^{-1} \ ^1\mathbf{v}\\ &= \mathbf{R}_{(n-1)n}^{-1} \cdots \mathbf{R}_{23}^{-1} \mathbf{R}_{23}^{-1} \ ^1\mathbf{v}\\ \sim \quad \mathbf{v}_n &= \mathbf{\tilde{R}}_{(n-1)n} \cdots \mathbf{\tilde{R}}_{23} \mathbf{\tilde{R}}_{12} \mathbf{v}_1 \end{align} \end{split}\]

Il est possible de lire cette opération de changement de bases comme une succession de rotations entre un vecteur \(\mathbf{v}_1\) de composantes égales à \(^1\mathbf{v}\) et un vecteur \(\mathbf{v}_n\) de composantes égales à \(^n\mathbf{v}\) où les sens de rotation entre les bases sont inversés par rapports aux rotations des vecteurs.

Exemple

Cette vision est explicitée sur un exemple par comparaison des figures Fig. 5, rotation du vecteur (« rotation active ») et Fig. 6, rotation équivalente de la base (« rotation passive ») :

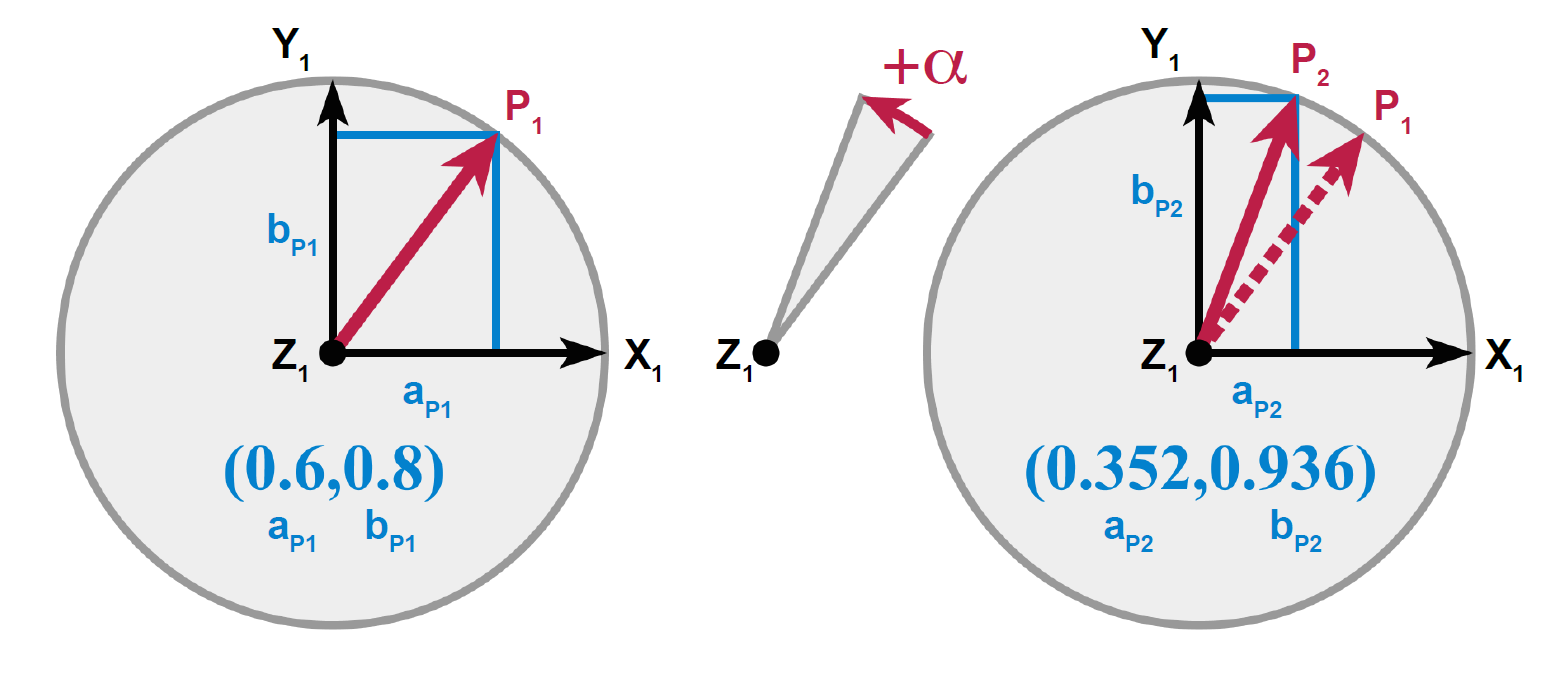
Fig. 5 Rotation du vecteur ; rotation dite « active »

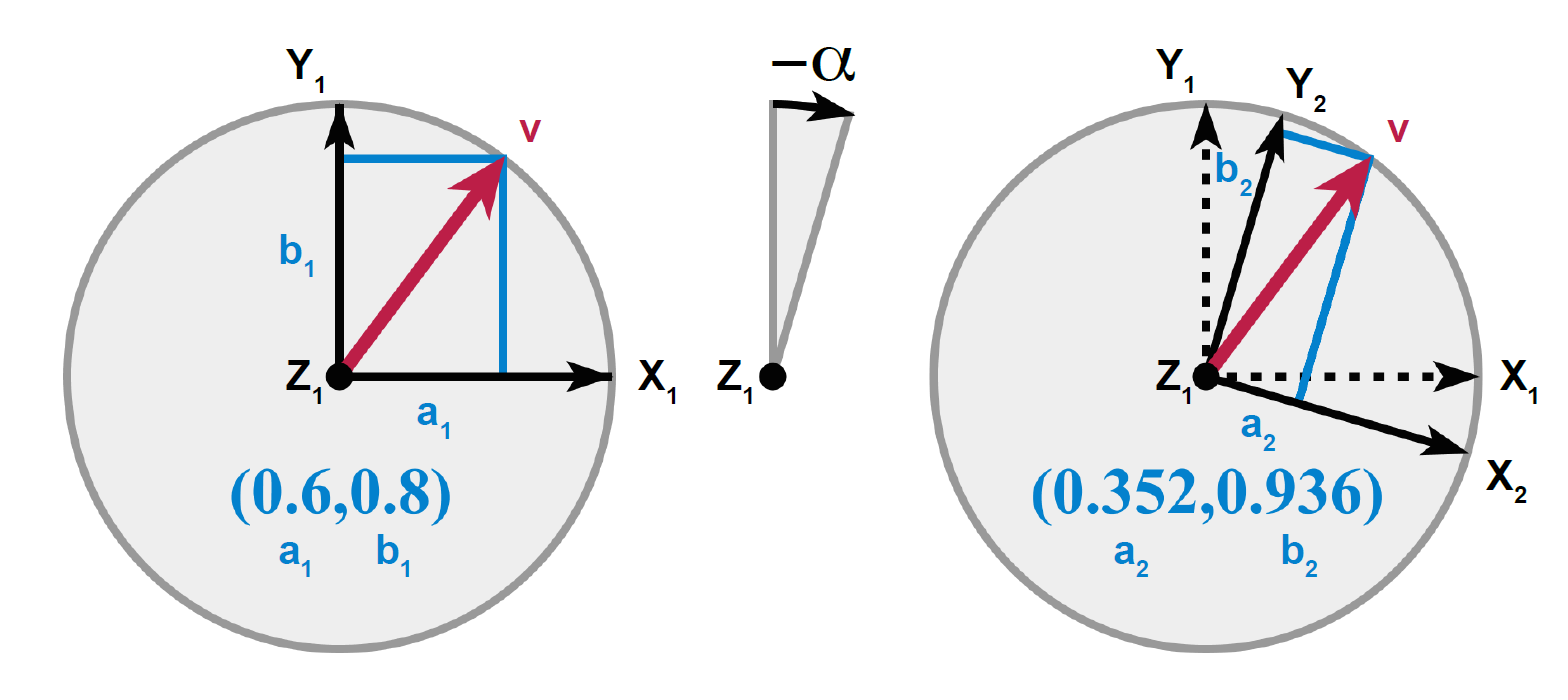
Fig. 6 Rotation inverse de la base d’expression ; rotation dite « passive »

Opérateur de changement de repère

Soient \(\mathbf{O}_1\) et \(\mathbf{O}_2\) les centres des repères 1 et 2 :

\[ \begin{equation} \mathcal{R}_1 = ( \mathbf{O}_1, \mathcal{B}_1 ) \quad \text{et} \quad \mathcal{R}_2 = ( \mathbf{O}_2, \mathcal{B}_2 ) \end{equation} \]

On cherche à exprimer un point \(P\) exprimé dans un repère \(\mathcal{R}_1\) (vecteur \(^1\mathbf{P}\)) à partir de ses coordonnées connues dans un repère \(\mathcal{R}_1\) (vecteur \(^2\mathbf{P}\)) :

\[\begin{split} \begin{equation} ^1\mathbf{P} = \begin{bmatrix} a_1 \\ b_1 \\ c_1 \end{bmatrix}_{\mathcal{R}_1} ^2\mathbf{P} = \begin{bmatrix} a_2 \\ b_2 \\ c_2 \end{bmatrix}_{\mathcal{R}_2} \end{equation} \end{split}\]

Connaissant les coordonnées du point \(O_2\) dans \(\mathcal{R}_1\) :

\[\begin{split} \begin{equation} ^2\mathbf{O}_2 = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}_{\mathcal{R}_1} \end{equation} \end{split}\]

les coordonnées du point \(P\) exprimées dans \(\mathcal{R}_1\) respectent la relation suivante :

(2)\[\begin{split} \begin{align} \overrightarrow{O_1 P} &= \overrightarrow{O_1 O_2} + \overrightarrow{O_2 P} \\ \Leftrightarrow ^1\mathbf{P} &= ^1\mathbf{O}_2 + \mathbf{R}_{12} \ ^2\mathbf{P} \end{align} \end{split}\]

Cette écriture fait apparaître clairement que l’opérateur de changement de repère comporte deux transformations successives :

• une « translation » de vecteur : addition de deux vecteurs,

• une « rotation » qui fait passer de la base \(\mathcal{B}_2\) à la base \(\mathcal{B}_1\) : opération de multiplication matricielle.

Transformation homogène

Expression d’un point de l’espace

L’opérateur homogène permet, par un simple jeu d’écriture, de condenser les opérations de rotation et de translation. Les coordonnées homogènes d’un point \(P\) dans un repère 3D \(\mathcal{R}\) s’écrivent sous la forme :

\[\begin{split} \begin{equation} \mathbf{P} = \begin{bmatrix} A \\ B \\ C \\ \omega \end{bmatrix} \end{equation} \end{split}\]

où \(\omega\) est un scalaire appelé « facteur d’homogénéité » \(\in \mathbb{R}^{*}\) pour un point à une distance finie (un point à distance infinie représente une direction de l’espace). La correspondance avec les coordonnées cartésiennes est obtenue par :

\[\begin{split} \begin{equation} \begin{cases} a = A/\omega \\ b = B/\omega \\ v = C/\omega \end{cases} \end{equation} \end{split}\]

Pour réduire l’infinité de quadruplés \((A, B, C, \omega)\) pour les coordonnées homogènes, on fixera par la suite la valeur de \(\omega\) à 1. L’expression du point \(P\) en coordonnées homogènes est donc :

\[\begin{split} \begin{equation} \mathbf{P} = \begin{bmatrix} A \\ B \\ C \\ 1 \end{bmatrix} \end{equation} \end{split}\]

Expression d’une direction de l’espace

Une direction de l’espace sous forme de coordonnées homogènes peut être vue comme un vecteur défini entre deux points :

\[\begin{split} \begin{equation} \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 = \begin{bmatrix} A_2 \\ B_2 \\ C_2 \\ 1 \end{bmatrix} - \begin{bmatrix} A_1 \\ B_1 \\ C_1 \\ 1 \end{bmatrix} = \begin{bmatrix} A_2 - A_1 \\ B_2 - B_1 \\ C_2 - C_1 \\ 0 \end{bmatrix} \end{equation} \end{split}\]

Par convention, la direction est définie comme un vecteur unitaire \(\overrightarrow{u}\) et la connaissance du sens est donnée par les valeurs de ses trois coordonnées \(u\), \(v\), \(w\). La notation d’une direction unitaire orientée en coordonnées homogènes est :

\[\begin{split} \begin{equation} \mathbf{u} = \begin{bmatrix} u \\ v \\ w \\ 0 \end{bmatrix} \end{equation} \end{split}\]

Complément sur les coordonnées homogènes

Pour être plus complet, une direction orientée est vue comme un point rejeté à l’infini (Fig. 7). On choisit la valeur « zéro » pour le facteur d’homogénéité, les valeurs \(A\), \(B\), \(C\) restent finies. Ainsi, le point \(P\) à l’infini a pour expression :

\[\begin{split} \begin{equation} \mathbf{P} = \begin{bmatrix} A \\ B \\ C \\ 0 \end{bmatrix} \end{equation} \end{split}\]

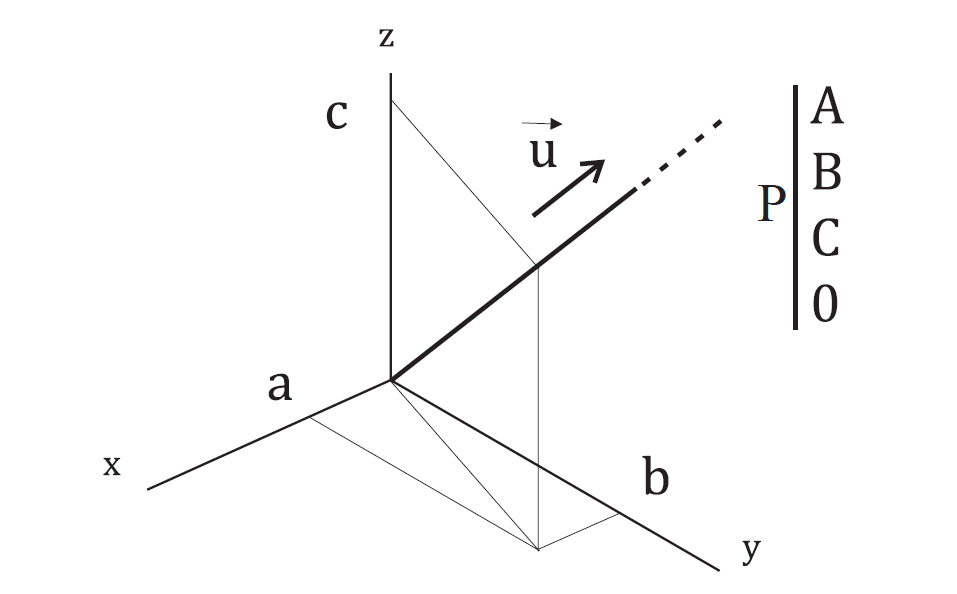
Fig. 7 Représentation d’un point à l’infini au sens des coordonnées homogènes ou d’une direction au sens de l’espace vectoriel

et ses coordonnées cartésiennes s’expriment :

\[\begin{split} \begin{equation} \begin{cases} a = A/0 \\ b = B/0 \\ v = C/0 \end{cases} \end{equation} \end{split}\]

Ainsi, les valeurs des coordonnées sont trois valeurs infinies dont les rapports 2 à 2 sont finis :

\[ \begin{equation} a/c = A/C \quad a/b = A/B \quad b/c = B/C \end{equation} \]

Le point \(P\) est à l’infini, mais la droite \((OP)\) a une direction bien définie. Il faut noter que cette droite n’est plus orientée. On peut adopter, pour les coordonnées \(A\), \(B\) et \(C\) tout ensemble de valeurs restant proportionnelles entre elles.

Changement de repère en coordonnées homogènes

On construit alors l’opérateur homogène comme une matrice \(4\times 4\) réalisant un changement de repère 3D, c’est à dire une rotation puis une translation :

\[\begin{split} \begin{equation} \begin{bmatrix} a_1 \\ b_1 \\ c_1 \\ 1 \end{bmatrix}_{\mathcal{R}_1} = \begin{bmatrix} & & & t_x \\ & \mathbf{R}_{12} & & t_y \\ & & & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} a_2 \\ b_2 \\ c_2 \\ 1 \end{bmatrix}_{\mathcal{R}_2} \end{equation} \end{split}\]

Le changement de repère peut ainsi se faire à l’aide d’une seule opération matricielle. L’opérateur homogène est formé par la juxtaposition des coordonnées homogènes des trois directions orientées du repère \(\mathcal{R}_2\) exprimées dans le repère \(\mathcal{R}_1\) \((\mathbf{R}_{12})\) et des coordonnées homogènes de l’origine \(O_2\) de \(\mathcal{R}_2\) dans \(\mathcal{R}_1\) \((\mathbf{t}_{12})\) :

\[\begin{split} \begin{equation} ^1\mathbf{P} = \mathbf{T}_{12}\ ^2\mathbf{P} \quad \text{avec} \quad \mathbf{T}_{12} = \begin{bmatrix} & & & \\ & \mathbf{R}_{12} & & \mathbf{t}_{12} \\ & & & \\ 0 & 0 & 0 & 1 \end{bmatrix} \quad \text{où} \quad \mathbf{t}_{12} = ^1\mathbf{O}_2 = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}_{\mathcal{R}_1} \end{equation} \end{split}\]

Il est nécessaire de faire attention à la transformation inverse qui ne s’écrit pas immédiatement, mais sous la forme :

\[\begin{split} \begin{equation} \mathbf{T}_{21} = \mathbf{T}_{12}^{-1} = \begin{bmatrix} & & & \\ & \mathbf{R}_{12}^t & & -\mathbf{R}_{12}^t \mathbf{t}_{12} \\ & & & \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation} \end{split}\]

car en effet, à partir de l’équation (2), l’expression de \(P\) dans le repère \(\mathcal{R}_2\) s’écrit :

\[\begin{split} \begin{align} ^1\mathbf{P} &= ^1\mathbf{O}_2 + \mathbf{R}_{12}\ ^2\mathbf{P} \\ \Leftrightarrow ^1\mathbf{P} -\ ^1\mathbf{O}_2 &= \mathbf{R}_{12}\ ^2\mathbf{P} \\ \Leftrightarrow \mathbf{R}_{12}^t\ ^1\mathbf{P} -\mathbf{R}_{12}^t\ ^1\mathbf{O}_2 &= \mathbf{R}_{12}^t\ \mathbf{R}_{12}\ ^2\mathbf{P} \\ \Leftrightarrow \mathbf{R}_{12}^t\ ^1\mathbf{P} - \mathbf{R}_{12}^t\ ^1\mathbf{t}_{12} &= \ ^2\mathbf{P} \end{align} \end{split}\]

On peut noter également que la succession de deux transformations homogènes \(\mathbf{T}_{12}\) et \(\mathbf{T}_{23}\) donne une transformation homogène :

\[\begin{split} \begin{align} \mathbf{R}_{12} = \mathbf{R}_{12} \mathbf{R}_{12} &= \begin{bmatrix} & & & \\ & \mathbf{R}_{12} & & \mathbf{t}_{12} \\ & & & \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} & & & \\ & \mathbf{R}_{23} & & \mathbf{t}_{23} \\ & & & \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} & & & \\ & \mathbf{R}_{12} \mathbf{R}_{23} & & \mathbf{t}_{12} + \mathbf{R}_{12} \mathbf{t}_{23} \\ & & & \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align} \end{split}\]

Il est important de rappeler que l’on ne peut permuter le produit des deux transformations :

\[ \begin{equation} \mathbf{T}_{12} \mathbf{T}_{23} \neq \mathbf{T}_{23} \mathbf{T}_{12} \end{equation} \]