Modèle statique

Introduction

L’objectif de ce chapitre est d’exprimer le lien entre les actions mécaniques extérieures qui s’exercent sur le robot, notamment au niveau de l’effecteur et les couples et forces articulaires au niveau de chaque liaison. On supposera dans la suite que seules les actions mécaniques s’exerçant sur le dernier corps solide \(n\) du robot sont considérées.

Représentation des actions mécaniques extérieures

Les actions mécaniques agissant sur l’effecteur sont exprimées par les deux composantes du torseur d’action mécanique, l’effort \(\mathbf{f}\) et le moment \(\mathbf{F}_i\) exprimé au point \(O_i\), origine du repère \(\mathcal{R}_i\) :

\[\begin{split} \begin{equation} \begin{cases} \mathbf{f} &= \mathbf{f}_{ext \rightarrow \mathcal{R}_i} \\ \mathbf{m}_i &= \mathbf{m}(O_i)_{ext \rightarrow \mathcal{R}_i} \end{cases} \end{equation} \end{split}\]

En écriture matricielle, les actions mécaniques s’exerçant en \(O_i\) peuvent être regroupées dans une même matrice \(\mathbf{F}_i\) prenant la forme :

\[\begin{split} \begin{equation} \mathbf{F}_i = \begin{bmatrix} \mathbf{m}_i\\ \mathbf{f} \end{bmatrix} \end{equation} \end{split}\]

Les expressions de ces composantes d’effort et de moment dans un nouveau repère \(\mathcal{R}_n\) , d’origine \(O_n\) sont données par les relations classiques de changement de base et de point d’expression :

\[\begin{split} \begin{align} ^n \mathbf{f} &= \mathbf{R}_{ni} \ ^i\mathbf{f} \\ ^n \mathbf{m}_i &= \mathbf{R}_{ni} \ ^i\mathbf{m}_n \\ ^n \mathbf{m}_i &= \mathbf{R}_{ni} ( ^i\mathbf{m}_i + ^i \mathbf{O}_n\mathbf{O}_i \wedge ^i\mathbf{i}) \end{align} \end{split}\]

Exprimées dans le système de coordonnées de la base \(\mathcal{B}_n\) du repère \(\mathcal{R}_n\) (et au point \(O_n\) pour la composante de moment), ces actions mécaniques extérieures s’écrivent :

\[\begin{split} \begin{equation} ^n \mathbf{F}_n = \begin{bmatrix} ^n \mathbf{m}_n\\ ^n \mathbf{f} \end{bmatrix} \end{equation} \end{split}\]

S’il est plus simple de conserver les actions mécaniques exprimées dans la base \(\mathcal{B}_0\), alors, on aboutira à :

\[\begin{split} \begin{equation} ^0 \mathbf{F}_n = \begin{bmatrix} ^0 \mathbf{m}_n\\ ^0 \mathbf{f} \end{bmatrix} \end{equation} \end{split}\]

Relation entre actions mécaniques des actionneurs et actions mécaniques externes

Afin de valider la faisabilité d’une tâche ou de dimensionner un robot, il peut être nécessaire d’exprimer les couples et efforts que doivent délivrer les actionneurs en fonction des actions mécaniques externes au robot qui s’exercent sur l’effecteur. Pour faire le lien entre actions mécaniques externes et internes, le principe des travaux virtuels permet d’écrire :

\[\begin{split} \begin{align} \Sigma W_{int} &= \Sigma W_{ext} \\ \Leftrightarrow \mathbf{\Gamma}^t \mathbf{dq} &= \begin{bmatrix} \mathbf{m}_n & \mathbf{f} \end{bmatrix} \begin{bmatrix} \delta_n \\ \mathbf{d}_n \end{bmatrix} \end{align} \end{split}\]

où \(\mathbf{\Gamma}\) représente le vecteur des couples et forces exercés par les actionneurs correspondants aux liaisons \(q\). En remplaçant le petites rotations et petits déplacements au niveau de l’effecteur par la jacobienne de base ((16)), on obtient :

(22)\[\begin{split} \begin{align} \mathbf{\Gamma}^t \mathbf{dq} &= \begin{bmatrix} \mathbf{m}_n & \mathbf{f} \end{bmatrix} \mathbf{J}_n \mathbf{dq} \\ \Leftrightarrow \mathbf{\Gamma}^t = \mathbf{F}_n^t \mathbf{J}_n \\ \Leftrightarrow \mathbf{\Gamma} = \mathbf{J}_n^t \mathbf{F}_n \end{align} \end{split}\]

Pour le calcul pratique, généralement on exprimera les actions mécaniques extérieures et jacobien de base soit dans la base associée à l’effecteur \(\mathcal{B}_n\)

\[ \begin{equation} \mathbf{\Gamma} = ^n \mathbf{J}_n^t \ ^n \mathbf{F}_n \end{equation} \]

soit dans celle associée à la base fixe \(\mathcal{B}_0\)

\[ \begin{equation} \mathbf{\Gamma} = ^0 \mathbf{J}_n^t \ ^n0 \mathbf{F}_n \end{equation} \]

Dualité cinématique - statique

Comme démontré par le principe du travail virtuel, la matrice jacobienne intervenant en statique est la même que celle définie pour la cinématique. Ainsi, l’équation (22) permet de remarquer les points suivants \cite{XXX} :

• Les efforts et couples des actionneurs sont déterminés de façon univoque à partir d’une action mécanique arbitraire exercée sur l’organe terminal : L’espace image de \(\mathbf{J}^t\), noté \(\mathcal{I}(\mathbf{J}^t)\) est l’ensemble des efforts et couples des actionneurs \(\mathbf{\Gamma}\) non nuls permettant de compenser des actions mécaniques exercées sur l’organe terminal.

• Certaines actions mécaniques exercés sur l’effecteur ne sont pas reprises par les actionneurs : Il s’agit du noyau de \(\mathbf{J}^t\), noté, \(\mathcal{N}(\mathbf{J}^t)\) donnant alors un vecteur \(\mathbf{\Gamma}\) nul ; ces actions mécaniques seront reprises et transmises au bâti par les liaisons.

• On peut remarquer par ailleurs que le noyau de \(\mathcal{N}(\mathbf{J}^t)\) est le complément orthogonal de \(\mathcal{I}(\mathbf{J})\) : il représente l’ensemble des directions selon lesquelles le robot ne peut pas engendrer de vitesse.

• Enfin, on peut remarquer que certaines actions des actionneurs \(\mathbf{\Gamma}\) ne peuvent venir équilibrer les actions mécaniques \(\mathbf{F}_n\). Ce domaine est le complément de l’espace \(\mathcal{I}(\mathbf{J}^t)\) : il correspond à des directions de l’espace du noyau \(\mathcal{N}(\mathbf{J}^t)\) (complément orthogonal de l’espace \(\mathcal{I}(\mathbf{J}^t)\).

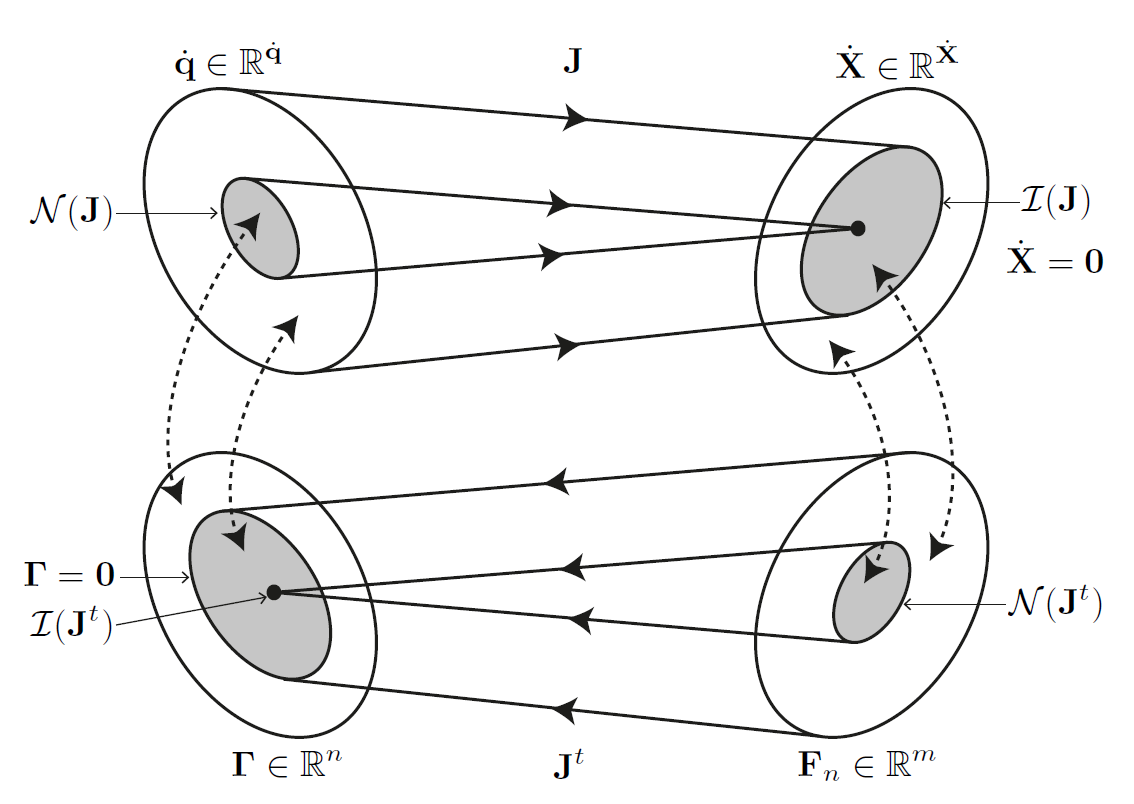
Fig. 20 Dualité vitesses - efforts d’après \cite{XXX}