Examen de Système Poly-Articulés - 2023/2024

On s’intéresse au robot spot produit par la société Boston Dynamics. Ce robot est composé de quatre jambes comprenant chacune 3 articulations. Le robot peut également être complété par un bras articulé au bout duquel se trouve une pince. Spot est un robot mobile agile qui navigue sur le terrain avec une mobilité sans précédent. Il permet ainsi d’automatiser des tâches d’inspection de routine et la capture de données de manière sûre, précise et fréquente.

Une description des composants du robot et de la pince sont donnés en annexe.

Fig. 79 Robot Spot + bras articulé

Étude d’une jambe : modèle géométrique direct

Le robot est composé de 4 jambes identiques. Ces 4 jambes sont reliées au corps du robot et sont chacune composées d’une hanche (hip), d’une jambe supérieure et d’une jambe inférieure (cf. Fig. 84). Les jambes ainsi que leurs composants sont désignés par leurs positions sur le robot « \(fl\) » pour front left « \(bl\) » pour back left et idem pour « \(fr\) » et « \(br\) ». Ces dénominations seront utilisées dans le paramétrage du robot. La distance entre les centres des articulations de la hanche (rouge) est nommée \(h_1\), la distance entre les articulations de la jambe supérieure (bleu) est notée \(h_2\) et la distance entre l’articulation et le pied (vert) est notée \(h_3\). La position du point \(O_{fl}\) dans le repère (\(O_{0}, \overrightarrow{x_0}, \overrightarrow{y_0}, \overrightarrow{z_0}\)) est notée (\(a_{fl}, b_{fl}, c_{fl}\)). Les pieds sont considérés comme des portions de sphère et leurs centres sont désignés par les points \(F_{fl}\), \(F_{bl}\) …

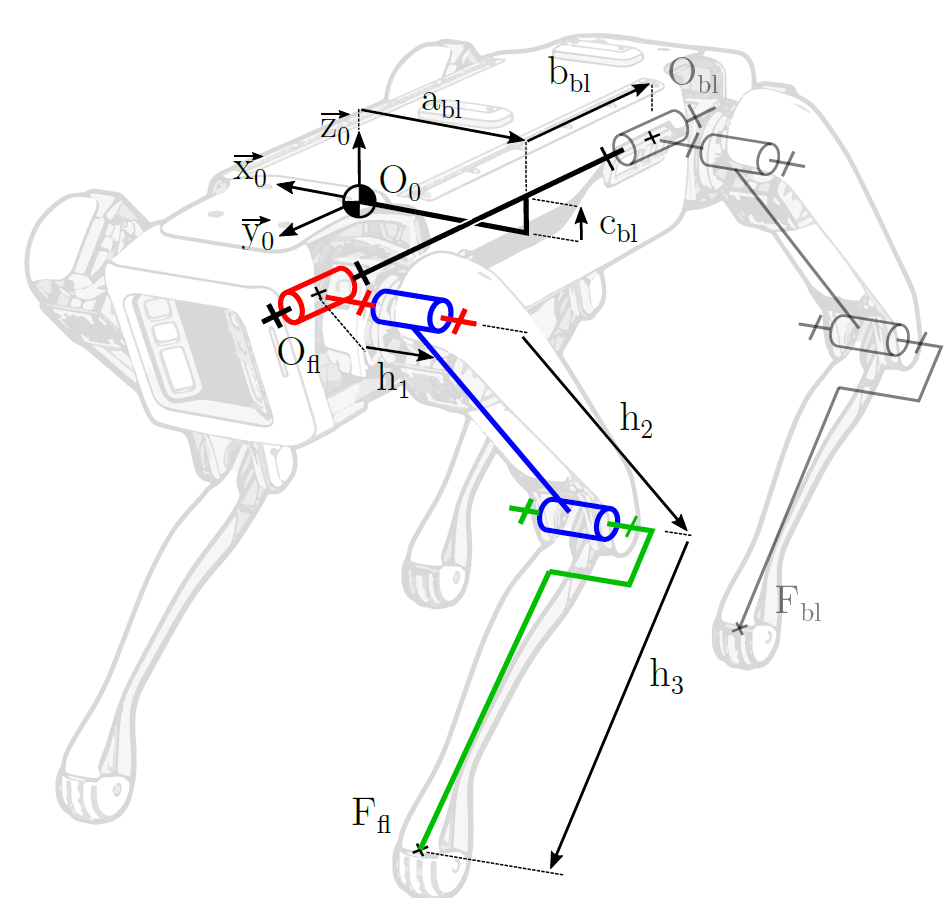
Fig. 80 Spot : schéma cinématique partiel

Question 1.1 : Construire sur le document réponse le paramétrage au sens de Denavit Hartenberg modifié (DHm) en partant du point \(O_{fl}\). On considèrera le repère de base de la jambe comme étant (\(O_{fl}, \overrightarrow{x_0}, \overrightarrow{y_0}, \overrightarrow{z_0}\)).

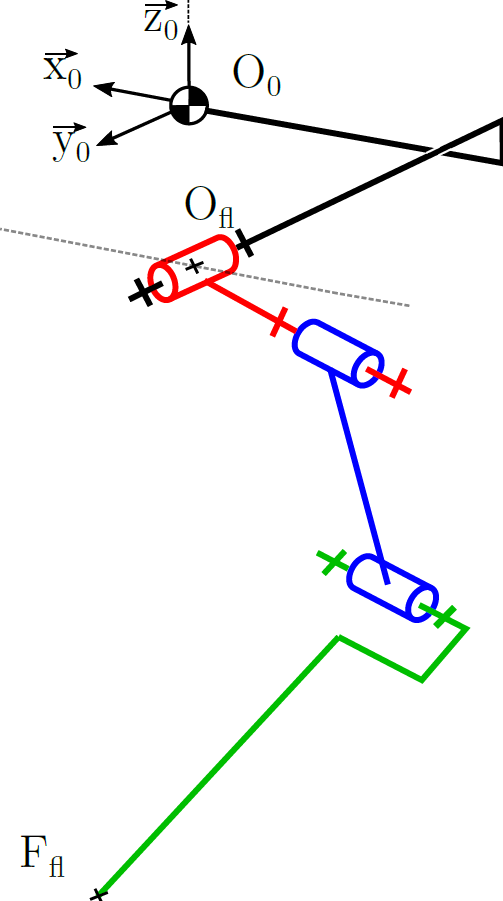
Fig. 81 Spot : schéma cinématique jambe avant gauche.

À titre indicatif : dans la Fig. 81 le trait en pointillé passant par \(O_{fl}\) est parallèle au vecteur \(\overrightarrow{x_0}\).

Question 1.2 : Synthétiser les résultats dans le tableau DHm associé. Dessiner également les figures de changement de repère en représentant les différents paramètres articulaires comme étant positif.

Question 1.3 : Déterminer les matrices homogènes de transformation \(T_{ij}\) entre les différents corps.

Question 1.4 : En déduire l’expression du modèle géométrique direct (MGD) permettant d’exprimer la position du pied avant gauche (\(x_{fl},y_{fl},z_{fl}\)) dans le repère du robot (\(O_{fl}, \overrightarrow{x_0}, \overrightarrow{y_0}, \overrightarrow{z_0}\)). Rappeler quels sont les paramètres de l’espace des tâches et les paramètres de l’espace articulaire.

Question 1.5 : Déterminer par le calcul les singularités de cette structure. Expliquer les solutions trouvées par des croquis pour expliquer le sens physique.

Étude d’une jambe : modèle géométrique inverse

Question 2.1 : En vous aidant de l’annexe 5.2, déterminer le modèle géométrique inverse en position uniquement permettant de relier les valeurs de \(\theta_i\) aux valeurs (\(x_{fl},y_{fl},z_{fl}\)).

Question 2.2 : Donner le nombre de configurations articulaires possibles pour une même position de l’effecteur (pied) sans tenir compte des limites articulaires. N’hésitez pas à expliquer votre raisonnement par des figures si nécessaire.

Question 2.3 : Les limites de chaque articulation sont données par le constructeur en annexe 5.1. En vous appuyant sur ces données, déterminez les relations entre les paramètres articulaires constructeurs et vos paramètres articulaires.

Question 2.4 : En tenant compte des limites articulaires, donner le nombre de configurations articulaires possibles pour une même position de l’effecteur (pied) (\(x_{fl},y_{fl},z_{fl}\)) dans le repère du robot (\(O_{fl}, \overrightarrow{x_0}, \overrightarrow{y_0}, \overrightarrow{z_0}\)).

Étude préliminaire du système complet

On s’intéresse maintenant au robot en considérant les pieds comme fixes. On souhaite orienter et positionner le corps du robot (\(O_{0}, \overrightarrow{x_0}, \overrightarrow{y_0}, \overrightarrow{z_0}\)) par rapport a un repère \(\mathcal{R}_f\) fixe liée au sol (\(O_{f}, \overrightarrow{x_f}, \overrightarrow{y_f}, \overrightarrow{z_f}\)). Les positions des 4 points F dans le repère \(\mathcal{R}_f\) sont connues. On considère que le MGI et le MGD des jambes sont connus.

Question 3.1 : Donner les paramètres de l’espace des taches et les paramètres de l’espace articulaire puis décrire de manière détaillée sans faire de calcul la méthode permettant d’obtenir le MGI du système entier (sans prendre en compte le bras articulé et la pince).

Question 3.2 : Le paramétrage permettant de définir l’orientation du corps du robot dans son environnement correspond à un paramétrage au sens de Tait Bryan (rotations X, Y”, Z””). S’agit-il d’un paramétrage extrinsèque ou intrinsèque ? Justifier.

Question 3.3 : Le fait d’assimiler le pied à un point présente-t-il un problème dans le paramétrage du robot. Justifier votre réponse.

Étude du bras articulé additionnel sans la pince

Dans cette dernière partie on s’intéresse uniquement au bras articulé représenté dans les Fig. 82 et Fig. 83.

Question 4.1 : Combien de degrés de liberté possède le bras articulé sans tenir compte de la pince.

Question 4.2 : En supposant connues toutes les matrices de transformation (\(T_{ij}\)) permettant de décrire le paramétrage géométrique du bras au sens de DHm, décrire précisément la démarche de résolution du MGI sans faire de calcul.

Annexes

Limites articulaires :

Limites articulaires de chaque jambe (les notations utilisées dans ce paragraphe ne sont utiles que pour la question 2.3):

• articulation 1 entre le corps et la hanche \(\theta_h\) : \(\pm\) 45 degrés par rapport au plan \((O_{fl},\overrightarrow{x_0},\overrightarrow{y_0})\)

• articulation 2 entre la hanche et la jambe supérieure \(\theta_u\) : entre + 41 et - 141 degrés par rapport à l’horizontale lorsque l’articulation 1 est a \(\theta_h = 0\).

• articulation 3 au niveau du genou entre la jambe supérieure et la jambe inférieure \(\theta_l\): entre -14 et - 160 degrés par rapport à la jambe tendue (flexion/extension de 14 à 160 degrés)

Équations :

Inverse d’une matrice homogène :

\[\begin{split} \begin{equation*} \mathbf{T}_{ij} = \begin{bmatrix} & & & \\ & \mathbf{R}_{ij} & & \mathbf{t}_{ij} \\ & & & \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \longrightarrow \mathbf{T}_{ji} = \begin{bmatrix} & & & \\ & \mathbf{R}_{ij} ^t & & -\mathbf{R}_{ij} ^t \mathbf{t}_{ij} \\ & & & \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{equation*} \end{split}\]

Solutions de l’équation de type 2 :

\[ \begin{equation*} X \text{S}\theta_i + Y \text{C}\theta_i = Z \end{equation*} \]

Solution :

\[\begin{split} \begin{align*} \theta_i = \begin{cases} \text{atan2}(\pm \sqrt{1 - \text{C}^2\theta_i},\, \text{C}\theta_i) \quad & \text{si} \quad X = 0 \text{ et } Y \ne 0 \\ \text{atan2}(\text{S}\theta_i, \, \pm \sqrt{1 - \text{S}^2\theta_i}) \quad & \text{si} \quad X \ne 0 \text{ et } Y = 0 \\ \begin{cases} \theta_{i1} = \text{atan2}(-Y,X) \\ \theta_{i2} = \theta_{i1} + 180\deg \end{cases} \quad & \text{si} \quad X \ne 0 \text{ et } Y \ne 0 \text{ et } Z = 0 \\ \text{atan2}(\text{S}\theta_i, \, \text{C}\theta_i) \quad & \text{si} \quad X \ne 0 \text{ et } Y \ne 0 \text{ et } Z \ne 0 \text{ et } X^2+Y^2 \geq Z^2 \\ \text{configuration singulière} \quad & \text{si} \quad X \ne 0 \text{ et } Y \ne 0 \end{cases} \end{align*} \end{split}\]

Dans le cas où \(X \ne 0\) et \(Y \ne 0\) et \(Z \ne 0\), l’équation est résolue en élevant l’expression au carré : en remplaçant les termes en sinus par les fonctions équivalentes en cosinus, on aboutit à une équation du second degré à résoudre donnant la valeur du cosinus. Un raisonnement analogue est mené pour déterminer le terme en sinus :

\[\begin{split} \begin{equation*} \begin{cases} \text{C}\theta_i = \dfrac{YZ - \varepsilon X \sqrt{X^2+Y^2-Z^2}}{X^2 + Y^2} \\ \text{S}\theta_i = \dfrac{XZ + \varepsilon Y \sqrt{X^2+Y^2-Z^2}}{X^2 + Y^2} \\ \end{cases} \qquad \text{avec} \qquad \varepsilon = \pm 1 \end{equation*} \end{split}\]

Dans ce cas, la résolution de l’équation donne deux solutions, correspondant aux valeurs de \(\varepsilon\).

Solutions de l’équation de type 6 :

\[\begin{split} \begin{equation*} \begin{cases} W\text{S}\theta_j = X\text{C}\theta_i + Y \text{S}\theta_i + Z_1 \\ W\text{C}\theta_j = X\text{S}\theta_i - Y \text{C}\theta_i + Z_2 \\ \end{cases} \end{equation*} \end{split}\]

Solution : Elle consiste à élever au carré chaque équation pour faire disparaître \(\theta_j\) en les additionnant.\(\theta_i\) est alors résolu par une équation de type 2. Ensuite, connaissant \(\theta_i\), \(\theta_j\) est déterminé par un système d’équations de type 3.

Solutions de l’équation de type 3 :

\[\begin{split} \begin{equation*} \begin{cases} X_1\text{s}\theta_i + Y_1 \text{c}\theta_i = Z_1 \\ X_2\text{S}\theta_i + Y_2 \text{C}\theta_i = Z_2 \\ \end{cases} \end{equation*} \end{split}\]

Dans le cas où \(X_1 Y_2 - X_2 Y_1 \neq 0\), les termes en cosinus et sinus sont obtenus par combinaison linaire des deux équations pour éliminer respectivement les termes sinus et cosinus :

\[\begin{split} \begin{equation*} \begin{cases} \text{C}\theta_i = \dfrac{Z_2 X_1 - Z_1 X_2}{X_1 Y_2 - X_2 Y_1} \\ \text{S}\theta_i = \dfrac{Z_1 Y_2 - Z_2 Y_1}{X_1 Y_2 - X_2 Y_1} \\ \end{cases} \end{equation*} \end{split}\]

Dans le cas où \(X_1 Y_2 - X_2 Y_1 = 0\) alors, les équations ne sont plus indépendantes ; on choisit alors l’une des deux équations que l’on résout en équation de type 2. Solution :

\[\begin{split} \begin{align*} \theta_i = \begin{cases} \text{atan2}(\text{S}\theta_i, \, \text{C}\theta_i) \quad & \text{si} X_1 Y_2 - X_2 Y_1 \neq 0 \\\text{atan2}(\dfrac{Z_1}{X_1} \, \dfrac{Z_2}{Y_2} ) \quad & \text{si} Y_1 = 0 \text{ et } X_2 = 0 \\ \end{cases} \end{align*} \end{split}\]

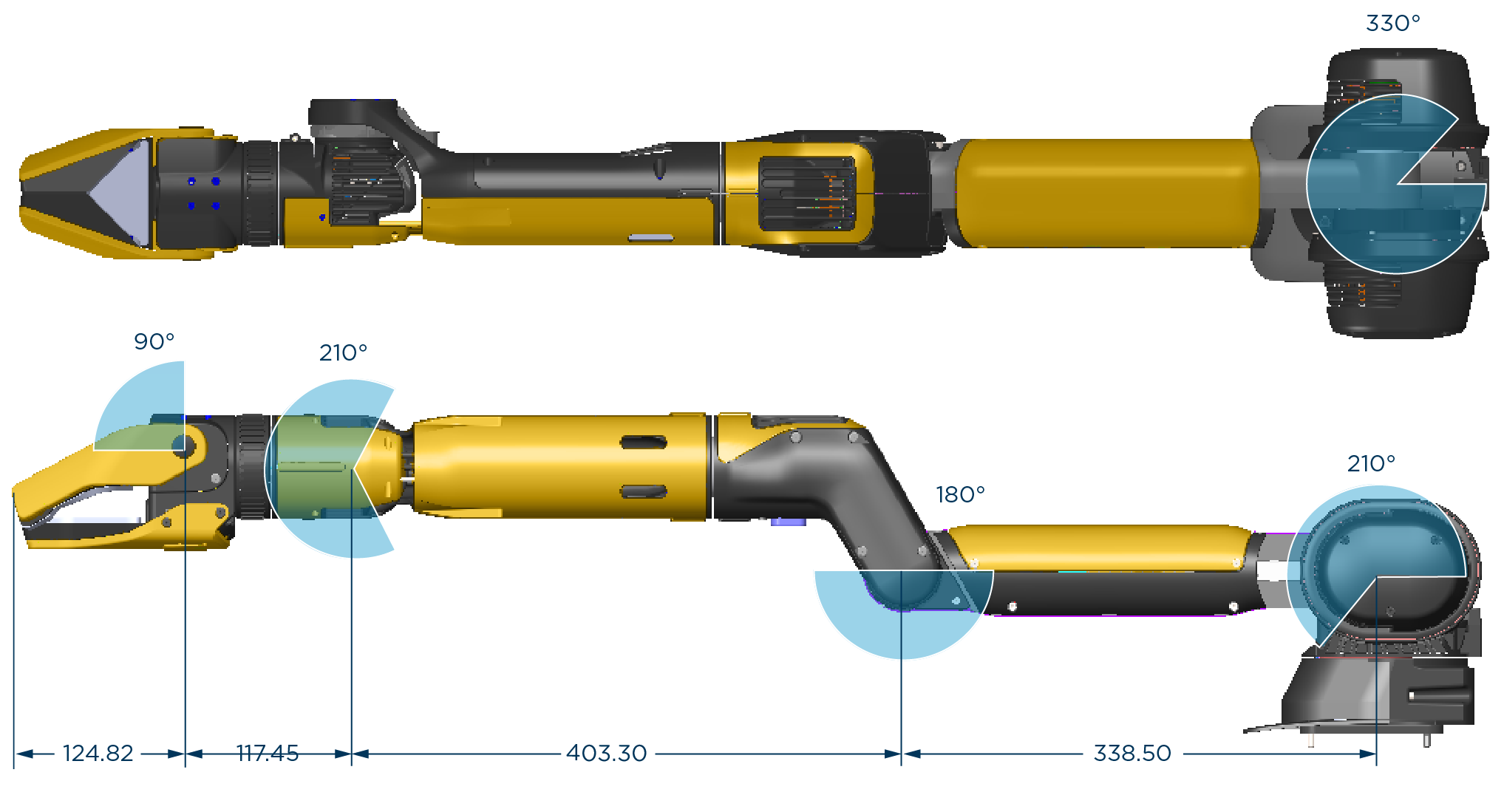
Fig. 82 Bras articulé : vue de dessus et vue de face

Fig. 83 Bras articulé : vue de côté

\begin{figure}[h!] \begin{center} \includegraphics[width=9.0cm]{spotanatomy.png} \caption{Spot : description des composants} \label{spot1} \end{center} \end{figure}

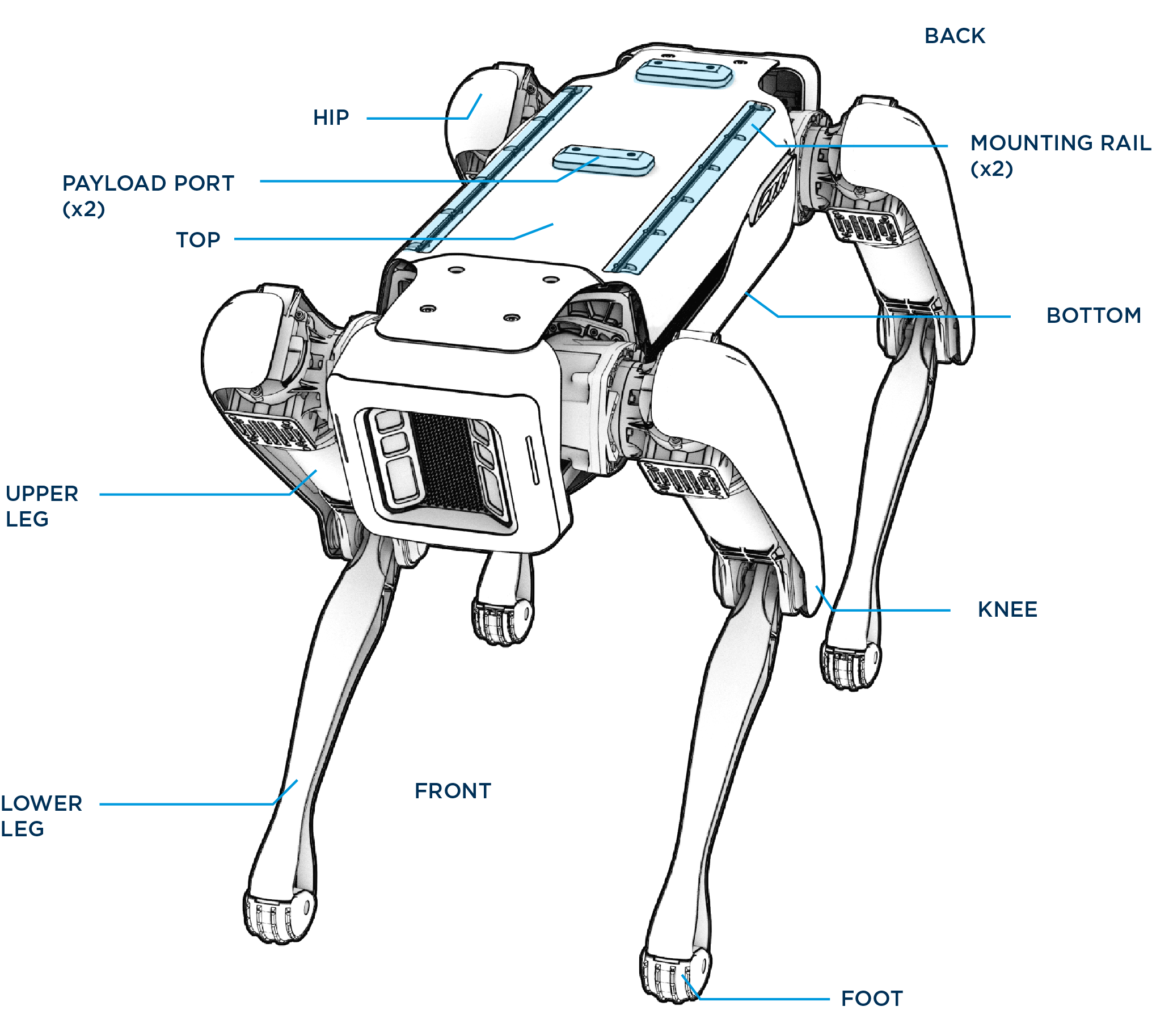
Fig. 84 Spot : description des composants

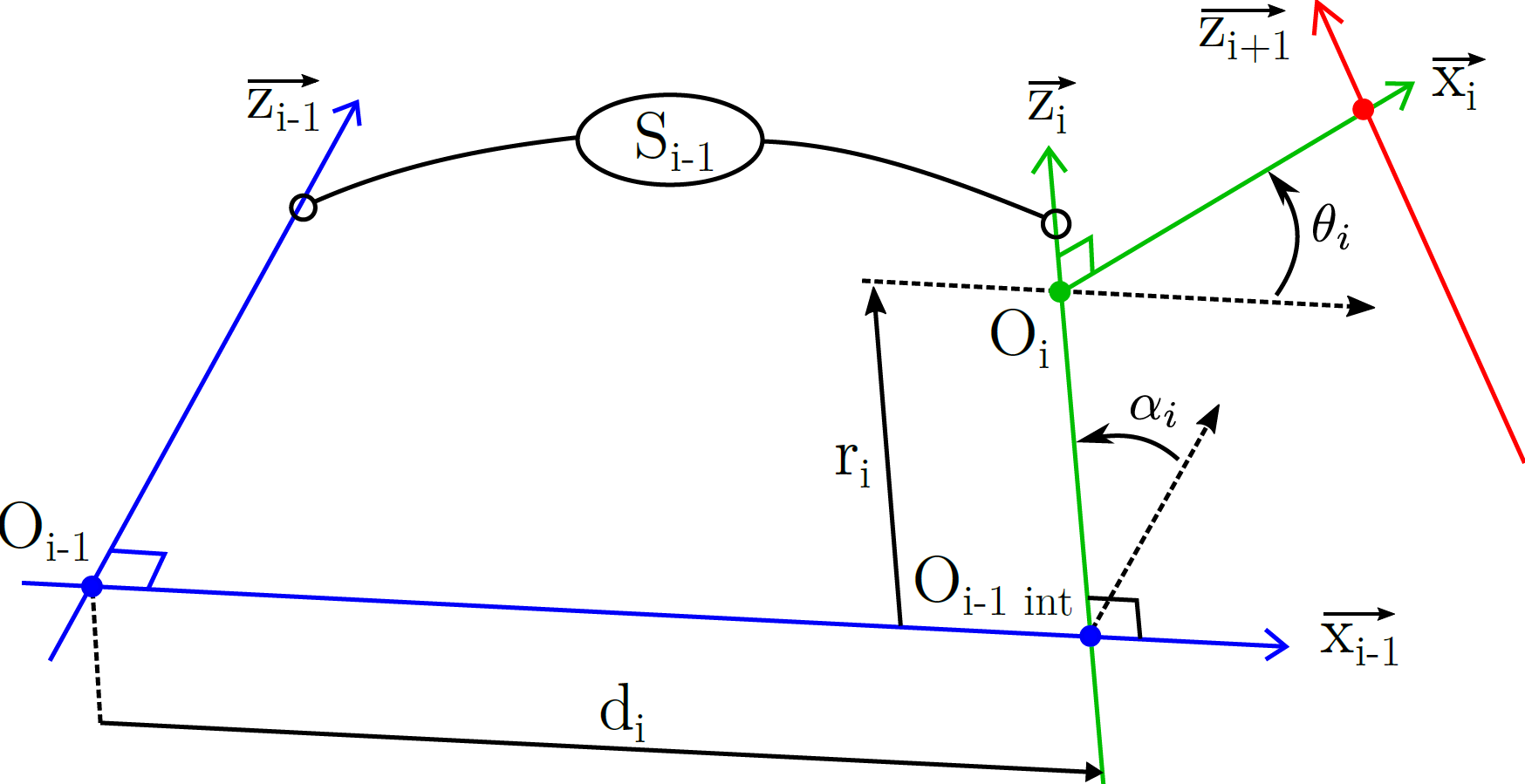
Fig. 85 Paramétrage de DHm