Décomposition en valeurs singulières (Singular Value Decomposition - SVD)

La décomposition en valeurs singulières permet de décomposer une matrice \(\mathbf{A}\) de dimensions \(m\times n\), de rang \(r\) en un produit de trois matrices faisant intervenir les valeurs singulières. Cette décomposition est définie pour des matrices à nombres réels ou complexes. Nous n’en donnerons ici qu’une application aux nombres réels.

\[ \begin{equation} \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^t \end{equation} \]

où

• \(\mathbf{U}\), de dimensions \(m\times m\), est une matrice orthogonale ;

• \(\mathbf{\Sigma}\), de dimensions \(m\times n\), est une matrice diagonale de rang r composée de réels positifs.

• \(\mathbf{V}^t\), de dimensions \(n\times n\), est une matrice orthogonale.

Les \(r\) réels non nuls composant la diagonale de \(\mathbf{\Sigma}\), notés \(\sigma_i\), sont les valeurs singulières de \(\mathbf{A}\), classées par ordre décroissant. Elles représentent les racines carrées des valeurs propres du produit \(\mathbf{A}^t \mathbf{A}\) ou \(\mathbf{A} \mathbf{A}^t\) selon que \(n < m\) ou \(n > m\) respectivement. La matrice \(\mathbf{\Sigma}\), associée à une matrice \(\mathbf{A}\) est unique. Les \(m\) colonnes de \(\mathbf{U}\) sont les vecteurs propres de \(\mathbf{A} \mathbf{A}^t\). Ils sont nommés « vecteurs singuliers à gauche » ou « vecteurs singuliers de sortie ». Les \(n\) colonnes de \(\mathbf{V}\) sont les vecteurs propres de \(\mathbf{A}^t \mathbf{A}\). Ils sont nommés « vecteurs singuliers à droite » ou « vecteurs singuliers d’entrée ».

La décomposition de la matrice pseudo inverse est donnée par la relation :

\[ \begin{equation} \mathbf{A}^{\dagger} = \mathbf{V} \mathbf{\Sigma}^{\dagger} \mathbf{U}^t \end{equation} \]

Lien au conditionnement

Cette décomposition SVD permet de déterminer directement le conditionnement en norme 2 de la matrice \(\mathbf{A}\) :

\[\begin{split} \begin{align} \text{Cond}_2 (\mathbf{A}) &= \lVert \mathbf{A} \rVert_2 \, \lVert \mathbf{A}^{\dagger} \rVert_2 \\ &= \sigma_{max}(\mathbf{A}) \sigma_{max}(\mathbf{A}^{\dagger}) \\ &= \frac{\sigma_{max}}{\sigma_{min}} \end{align} \end{split}\]

Interprétation géométrique

Étant donné que \(\mathbf{U}\) est une matrice orthogonale, les vecteurs colonnes qui la composent \((\mathbf{U}_i, \cdots, \mathbf{U}_m)\) constituent une base orthonormée de \(\mathbb{R}^m\). De même, les vecteurs, \((\mathbf{V}_i, \cdots, \mathbf{V}_n)\) constituent une base orthonormée de \(\mathbb{R}^n\).

Soit l’application linéaire \(T\) telle que :

\[\begin{split} \begin{equation} \begin{cases} T : \mathbb{R}^n \rightarrow \mathbb{R}^m \\ x \mapsto \mathbf{A} x \end{cases} \end{equation} \end{split}\]

Au sein des deux bases orthonormées, l’application \(T\) vérifie :

\[ \begin{equation} T(\mathbf{V}_i) = \sigma_i \mathbf{U}_i, \qquad i = 1, \cdots , \text{min}(m,n) \end{equation} \]

Il est donc possible de trouver deux bases orthonormées de \(\mathbb{R}^n\) et \(\mathbb{R}^m\) telle que l’application linéaire \(T\) transforme le ième vecteur de \(\mathbb{R}^n\) en un multiple non nul du ième vecteur de la base de \(\mathbb{R}^m\).

Pour visualiser simplement cette transformation, considérons la sphère unité de \(\mathbb{R}^n\). L’application linéaire \(T\) transforme la sphère en un ellipsoïde de \(\mathbb{R}^m\). Les valeurs singulières représentent les longueurs des demi-axes de cette ellipsoïde. Dans le cas particulier ou \(n = m\) et que toutes les valeurs singulières sont distinctes et non nulles la SVD peut être interprétée comme une succession de trois transformations (Fig. 21) :

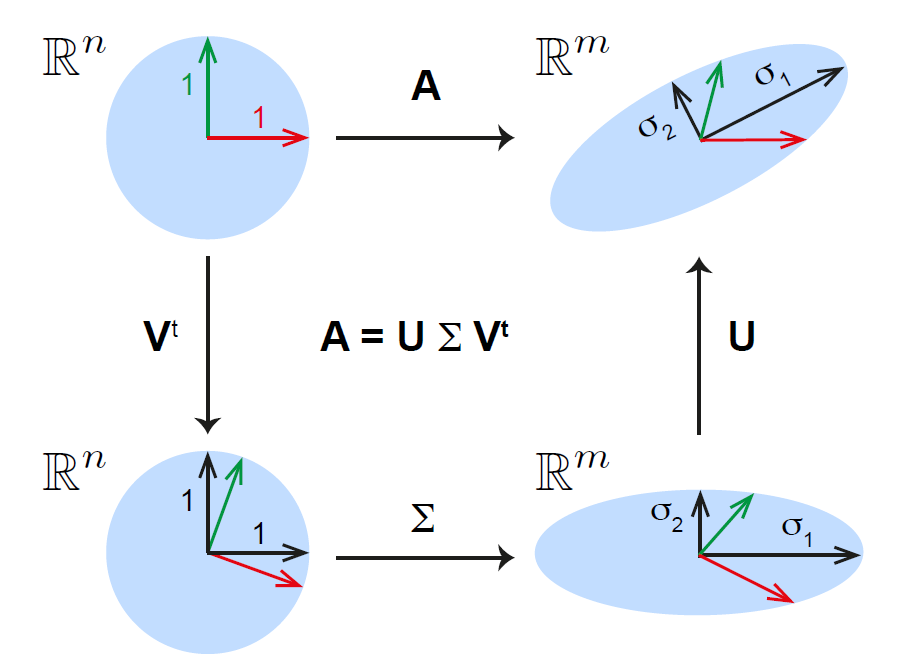
Fig. 21 Interprétation géométrique de la décomposition SVD

1. La première transformation \(\mathbf{V}^t\) effectue une rotation de la sphère unité ;

2. Ensuite, \(\mathbf{\Sigma}\) déforme la sphère unité sur chaque direction principale par la valeur singulière non nulle \(\sigma_i\). L’ellipsoïde est formé et orienté dans la base des vecteurs propres de \(\mathbf{\Sigma}\);

3. Enfin, \(\mathbf{U}\) réoriente à son tour l’ellipsoïde.