Ctrl+K

TD n°1 : Parmétrage - MGI, MGD d’un robot SCARA

TD n°1 : Parmétrage - MGI, MGD d’un robot SCARA#

On étudie le robot Scara 4 axes, référencé « s600 » de marque Adept.

../_images/photo_SCARA.png

Fig. 23 Robot SCARA s600#

Paramétrage#

Question 1.1 : En se basant sur la documentation technique fournie en Annexes, proposer un schéma cinématique de ce robot.

Question 1.2 : Construire sur le schéma, la paramétrisation au sens de Denavit et Hartenberg modifée. Synthétiser les résultats dans le tableau associé.

Question 1.3 : Déterminer chaque matrice homogène de transformation \(\mathbf{T}_{ij}\) entre les différents corps.

Question 1.4 : En déduire l’expression de la transformation globale permettant de passer d’un vecteur exprimé dans le référentiel associé à l’effecteur \(\mathcal{R}_{\text{eff.}}\), à son expression dans le référentiel associé à la base du robot \(\mathcal{R}_0\) :

\[ \begin{equation} {}^0\mathbf{P} = \mathbf{T_{0\,\text{eff}}} \, {}^\text{eff}\mathbf{P} \end{equation} \]

Question 1.5 : Retrouver par un raisonnement géométrique simple les équations définissant le vecteur translation entre le repère \(\mathcal{R}_0\) et le repère de l’effecteur \(\mathcal{R}_{\text{eff.}}\).

Modélisation Géométrique Directe et Inverse#

Question 2.1 : Proposer un paramétrage du repère effecteur \(\mathcal{R}_{\text{eff}}\) par rapport au repère de base \(\mathcal{R}_0\).

Question 2.2 : En étudiant successivement le problème en orientation puis en position, exprimer le MGD.

Question 2.3 : A l’aide des formulations géométriques données en Annexe des « Notes de cours » , exprimer le MGI.

Synthèse#

Question 3.1 : Analyser le modèle du robot implémenté dans l’application « RoboDK ».

Annexes#

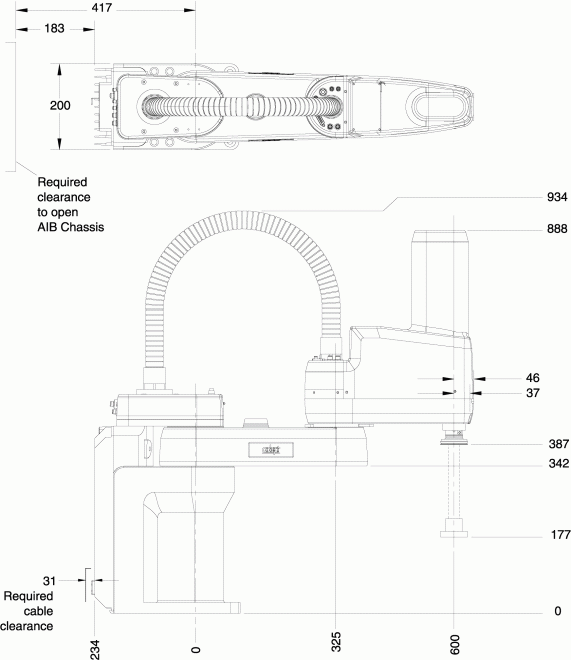
../_images/vue_cote.png

Fig. 24 Caractéristiques dimensionnelles#

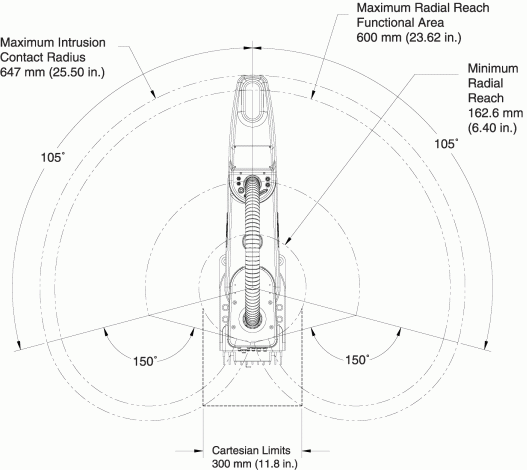
../_images/volume.png

Fig. 25 Surface balayée par l’effecteur#

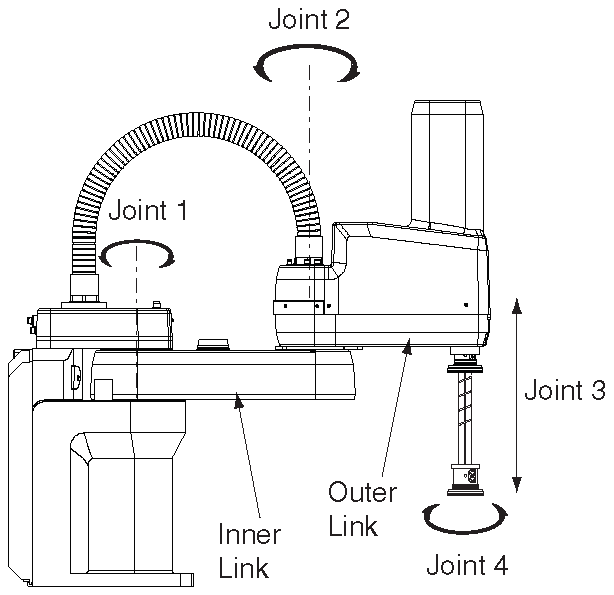
../_images/cinematique.png

Fig. 26 Extrait de documentation : cinématique#

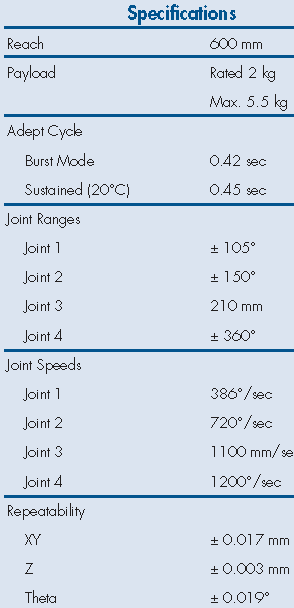
../_images/specifications.png

Fig. 27 Extrait de documentation : spécifications#

Contenu