TP : Étude d’un robot parallèle - Falcon#
Le robot Falcon de la société Novint (Fig. 64) est un système permettant à un opérateur d’interagir avec un environnement virtuel simulé sur un ordinateur. Ce dispositif, appelé « interface haptique », permet de fournir à l’environnement virtuel des informations de type déplacements et efforts, découlant de l’action de l’opérateur. En retour, le système renvoie à l’opérateur des effets de type effort mécanique (retour d’efforts) dont la fréquence et l’amplitude reproduisent les sensations réelles du toucher.
Ce système est utilisé dans différents contextes comme le jeu vidéo sur ordinateur, les simulateurs (militaire, chirurgicaux, dentaires…) ainsi que la télémanipulation et télérobotique (pilotage à distance par association de deux robots, un maître, l’autre esclave).

Fig. 64 robot haptique Falcon#
Découverte et prise en main du système#
L’objet de cette partie est de appréhender le système, son utilisation, son fonctionnement et ses potentialités au travers de manipulations élémentaires et analyse de documents ressources.
Question 1.1 : Mettre en oeuvre le système par quelques manipulations élémentaires (déplacements de la poignée); observer le comportement des composants.
Question 1.2 : A l’aide des documents ressources et du système, repérer les différents composants, décrire leurs fonctions ainsi que le fonctionnement global du système.
Question 1.3 : Analyser en détail la solution retenue par le fabricant concernant les capteurs. Expliquer leur principe de fonctionnement. Préciser notamment comment est repéré le « zéro » pour la position angulaire de l’axe.
Paramétrage du mécanisme#
L’objet de cette partie est de mettre en place un paramétrage sur le mécanisme permettant de repérer les positions de chaque composant en vue de la construction des modèles géométriques directs et inverses.
Question 2.1 : Proposer un modèle cinématique 3D pour le mécanisme (on ne représentera les liaisons que pour un seul bras).
Question 2.2 : Déterminer le degré d’hyperstatisme du modèle cinématique non minimal, pour le système entier constitué des trois bras. Conclure quant aux conséquences sur le système réel et aux solutions constructives.
Question 2.3 : A partir de la ~Fig. 68, proposer un paramétrage complet.
Question 2.4 : Quels sont les paramètres de l’espace des tâches ? Quels sont les paramètres de l’espace articulaire ? Quels sont les paramètres constants ?
Étude des modèles géométriques inverses et directs#
Modèle Géométrique Inverse (MGI)#
Question 3.1 : Proposer, sans la mettre en oeuvre totalement, une démarche pour expliciter la position angulaire de chaque moteur en fonction du positionnement de la poignée (cette fonction est le Modèle Géométrique Inverse).
Question 3.2 : Analyser les arguments d’entrée et de sortie de la fonction « MGI Falcon.m » fournie (il n’est pas demandé de comprendre le code à l’intérieur de la fonction, car complexe).
Question 3.3 : Exécuter la fonction « MGI Falcon.m » fournie ; observer les résultats numériques affichés dans la ligne de commande Matlab et la représentation graphique réalisée.
Question 3.4 : Parmi l’ensemble des solutions articulaires calculées et représentées, expliquer comment il est possible de déterminer l’unique solution viable.
Modèle Géométrique Direct (MGD)#
Pour les robots à architecture parallèle, le MGD est plus compliqué à déterminer que le MGI. Pour l’architecture du robot haptique Falcon, la résolution formelle du MGD fait appel a de multiples solutions issues de polynômes de degrés très élevés. Il est donc nécessaire par la suite de les trier pour ne conserver que la solution physiquement atteignable, en regard de la configuration physique du robot « précédente ».
Question 3.5 : Analyser les arguments d’entrée et de sortie de la fonction « MGD Falcon.m » fournie (il n’est pas demandé de comprendre le code à l’intérieur de la fonction, car complexe).
Question 3.6 : Exécuter la fonction « MGD Falcon.m » fournie; observer les résultats numériques affichés dans la ligne de commande Matlab et les représentations graphiques réalisées.
Question 3.7 : Parmi l’ensemble des positionnements de la plateforme mobile calculées et représentées (la poignée), retrouver la solution recherchée (qui est l’entrée du MGI).
Question 3.8 : Dans un contexte de commande du robot pour faire décrire à la plateforme mobile une trajectoire particulière, expliquer comment, à chaque temps de cycle du calculateur, choisir la solution parmi toutes celles calculées.
Modèle Géométrique Direct (MGD)#
Il est parfois utile d’avoir recours à des résolutions numériques, plutôt qu’à des résolutions formelles parfois inexistantes. Dans le cas du robot Falcon, la quantité et la complexité des calculs nécessaires à la résolution « exacte » ne permettent pas une implantation dans de petits processeurs temps-réel.
L’objet de cette partie est d’analyser et construire une solution numérique pour le calcul du MGD, en se basant sur le MGI. Pour simplifier l’approche, on considère le système dans une position particulière de la poignée, centrée sur le mécanisme (\(X=Y=0\)).
Question 3.9 : Exprimer la position \(Z\) du centre poignée pour une position angulaire moteur donnée. Utiliser les hypothèses définies ci-dessus pour simplifier l’écriture du MGD.
Question 3.10 : Tracer la courbe de la position angulaire du moteur, fonction de la position en \(Z\) (de \(Z_{min}=0.063 m\) à \(Z_{max}=0.183 m\)).
Question 3.11 : Proposer un algorithme pour déterminer le MGD à partir du MGI.
On considère maintenant que la poignée peut prendre n’importe quelle position \(X\),\(Y\), \(Z\) dans le volume atteignable.
Question 3.12 : Quelles sont les conséquences ou modifications par rapport au problème précédent? Proposer des évolutions à apporter à votre algorithme (sans les implémenter).
Documents ressources#
Les pages suivantes regroupent un certain nombre de documents permettant d’appréhender le fonctionnement du système ainsi que ses composants technologiques.

Fig. 65 Vue arrière du robot sans la carte électronique#

Fig. 66 Détails de la carte électronique#

Fig. 67 Zoom sur le codeur#
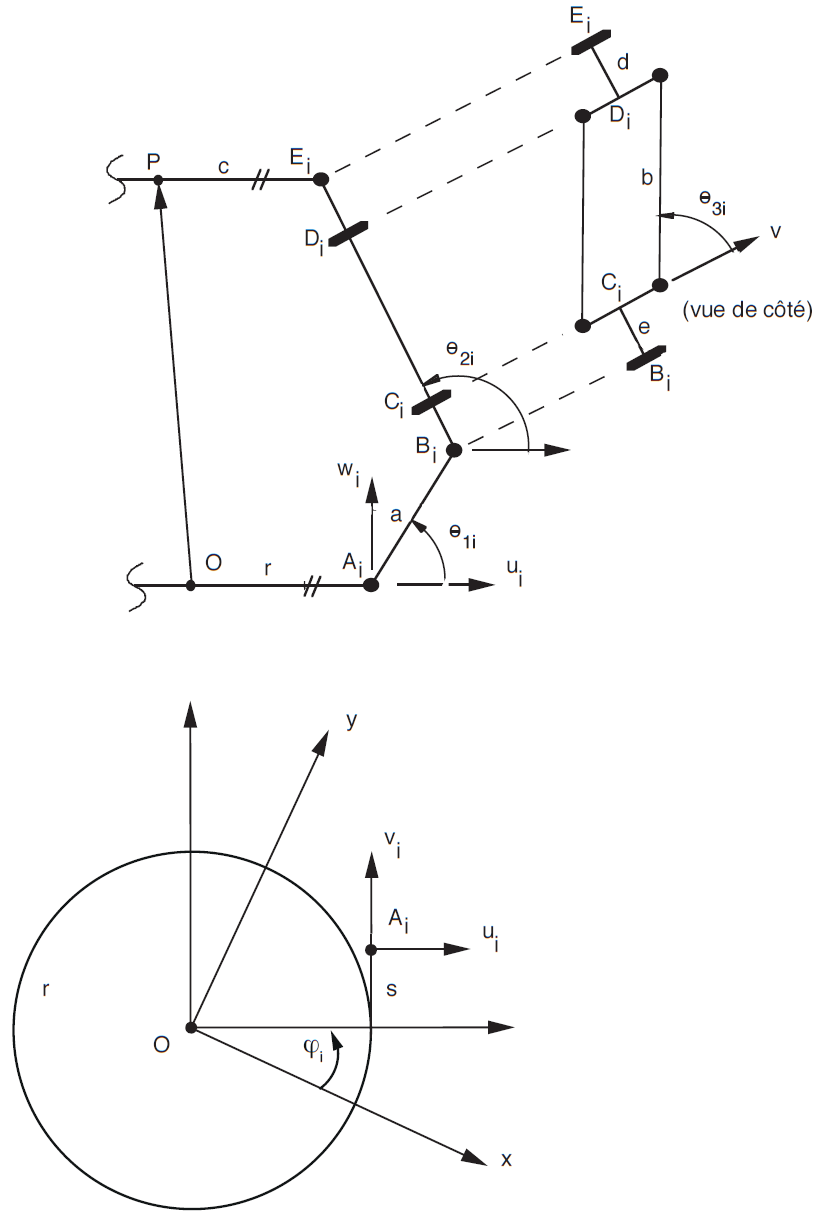
Fig. 68 Schéma de principe et paramétrage partielle#
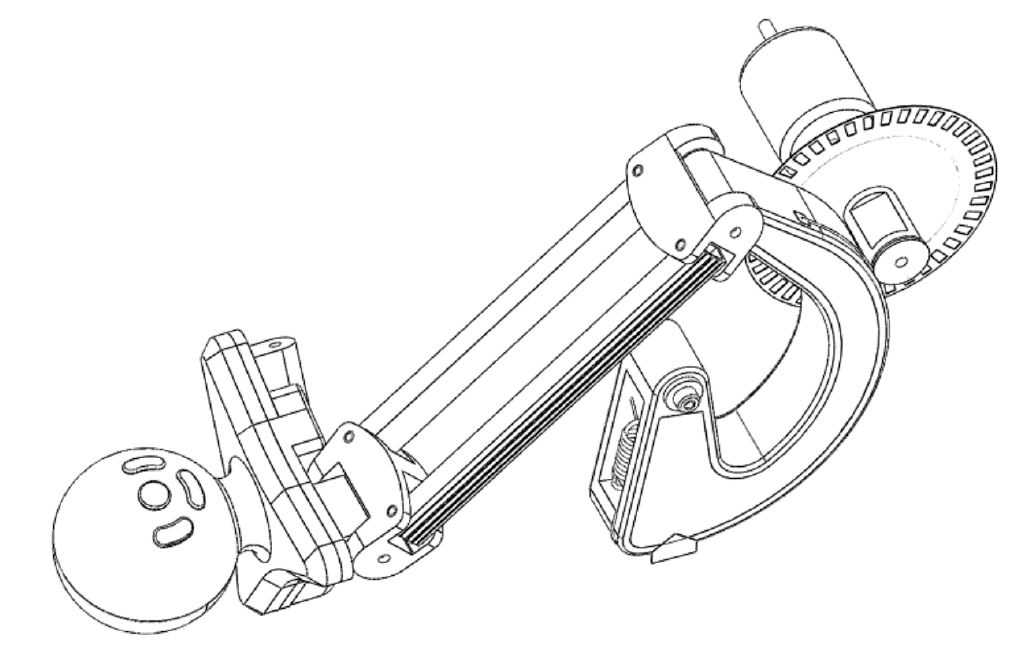
Fig. 69 Vue partielle de côté (plane pour un bras) dans la configuration centre de la poignée \(X=Y=0\), \(Z\) mini#
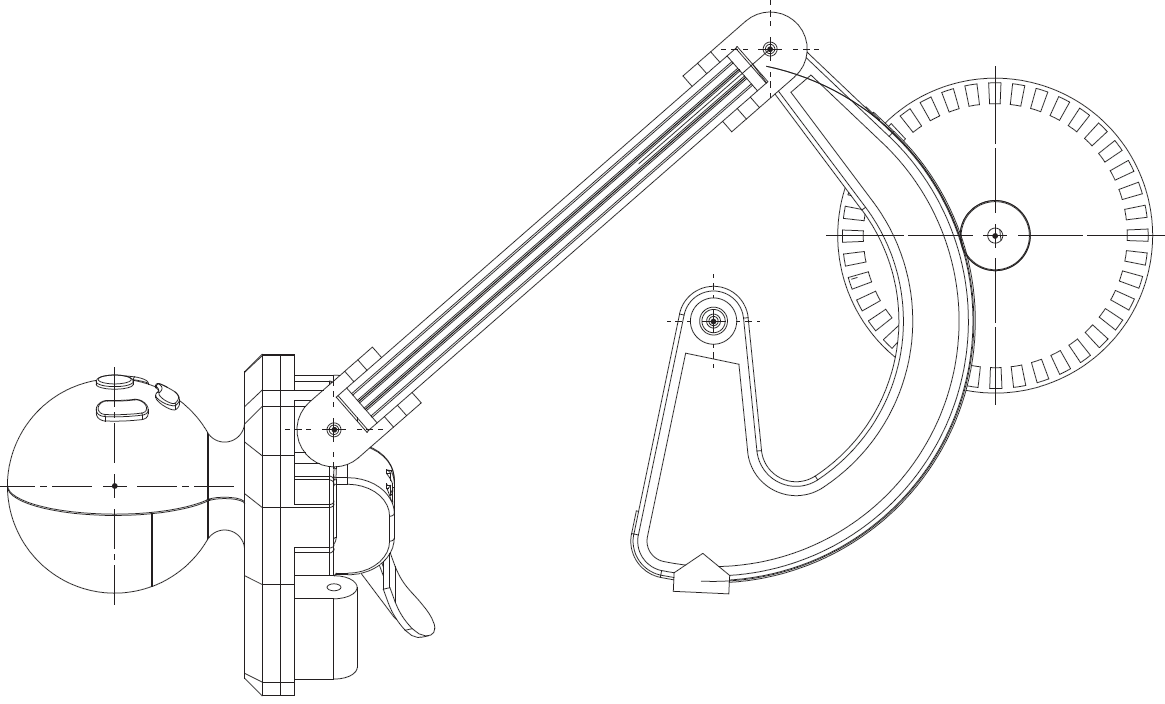
Fig. 70 Vue partielle de côté (plane pour un bras) dans la configuration centre de la poignée \(X=Y=0\), \(Z\) mini#
