Paramétrage des positionnements

Description des positions

Pour quasiment tous les constructeurs de robots, la position de l’effecteur est représentée par les coordonnées cartésiennes \((x, y, z)\). Très peu utilisent la représentation par coordonnées cylindriques ou sphériques (bien que parfois plus intéressant).

Description des orientations

Pour décrire l’orientation de l’effecteur, on trouve classiquement quatre représentations :

• les cosinus directeurs ;

• les angles d’Euler ;

• les angles de Bryan (roulis-tangage-lacet) ;

• les paramètres de Rodrigues (quaternions).

Cosinus directeurs

Soient deux bases : \(\mathcal{B}_0\) supposée fixée et \(\mathcal{B}_n\) liée au corps à paramétrer en orientation. Pour un vecteur particulier \(\mathbf{u}\), les cosinus directeurs de ce vecteur sont ses coordonnées exprimées dans \(\mathcal{B}_0\) :

\[\begin{split} \begin{equation} ^0\mathbf{u} = \begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix}_{\mathcal{B}_0} \end{equation} \end{split}\]

Pour représenter complètement l’orientation de \(\mathcal{B}_n\) par rapport à \(\mathcal{B}_0\), on peut exprimer dans \(\mathcal{B}_0\) les cosinus directeurs de chaque vecteur définissant \(\mathcal{B}_n\). On aboutit donc à 9 termes, ce qui rend bien évidemment ce paramétrage redondant :

\[\begin{split} \begin{equation} \mathbf{R}_{0n} = \begin{bmatrix}^0\mathbf{x}_n\ ^0\mathbf{y}_n\ ^0\mathbf{z}_n\ \end{bmatrix}_{\mathcal{B}_0} = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}_{\mathcal{B}_0} \end{equation} \end{split}\]

Angles d’Euler

La transformation permettant de passer de \(\mathcal{B}_0\) à \(\mathcal{B}_n\) est faite par les trois rotations successives suivantes, passant par les bases intermédiaires \(\mathcal{B}_i\) et \(\mathcal{B}_{ii}\) (Fig. 8) :

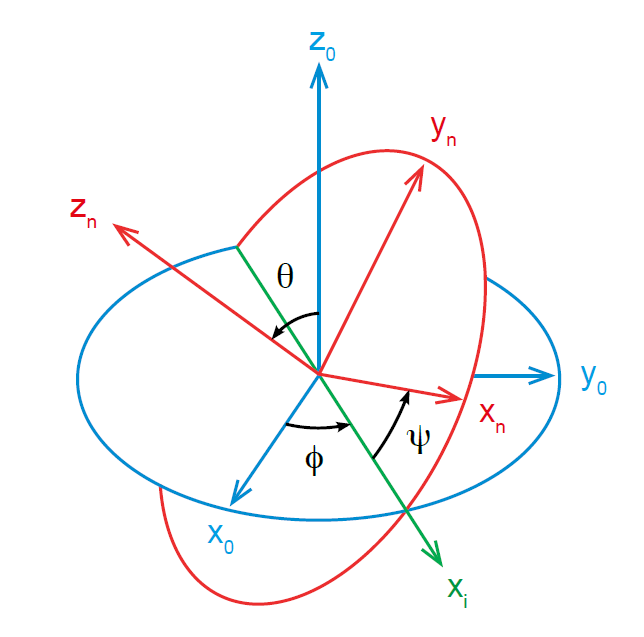
Fig. 8 Angles d’Euler : définition des rotations successives

\[\begin{split} \begin{align*} \mathcal{B}_0 \longrightarrow \mathcal{B}_i & \qquad \qquad \text{puis} & \mathcal{B}_i \longrightarrow \mathcal{B}_{ii} & \qquad \qquad \text{puis} & \mathcal{B}_{ii} \longrightarrow \mathcal{B}_{n}\\ \text{rot} \left(\overrightarrow{z_0}, \phi \right) & & \text{rot} \left(\overrightarrow{x_i}, \theta \right) & & \text{rot} \left(\overrightarrow{z_{ii}}, \psi \right) \end{align*} \end{split}\]

• une rotation autour de \(\overrightarrow{z_0} \), d’angle \(\phi \in \left[0, 360^{\circ} \right[\) (angle de précession) ;

• une rotation autour de \(\overrightarrow{x_i} \), d’angle \(\theta \in \left[0, 180^{\circ} \right]\) (angle de nutation) ;

• une rotation autour de \(\overrightarrow{z_{ii}} \), d’angle \(\psi \in \left[0, 360^{\circ} \right[\) (angle de rotation propre).

On peut remarquer que ce paramétrage met en oeuvre des rotations successives sur des bases intermédiaires, donc mobiles. Ce qui donne :

\[\begin{split} \begin{equation} \mathbf{R}_{0n} = \begin{bmatrix} \text{C}\phi & -\text{S}\phi & 0 \\ \text{S}\phi & \text{C}\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \text{C}\theta & -\text{S}\theta \\ 0 & \text{S}\theta & \text{C}\theta \end{bmatrix} \begin{bmatrix} \text{C}\psi & -\text{S}\psi & 0 \\ \text{S}\psi & \text{C}\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{equation} \end{split}\]

(3)\[\begin{split} \begin{equation} \Leftrightarrow \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} = \begin{bmatrix} \text{C}\phi\text{C}\psi-\text{S}\phi\text{C}\theta\text{S}\psi & -\text{C}\phi\text{S}\psi-\text{S}\phi\text{C}\theta\text{C}\psi & \text{S}\phi\text{S}\theta \\ \text{S}\phi\text{C}\psi+\text{C}\phi\text{C}\theta\text{S}\psi & -\text{S}\phi\text{S}\psi+\text{C}\phi\text{C}\theta\text{C}\psi & -\text{C}\phi\text{S}\theta \\ \text{S}\theta\text{S}\psi & \text{S}\theta\text{C}\psi & \text{C}\theta \end{bmatrix} \end{equation} \end{split}\]

Résolution inverse

L’objectif est de déterminer les valeurs des trois angles \(\phi\), \(\theta\) et \(\psi\) et à partir des cosinus directeurs \(r_{ij}\) la matrice de rotation globale \(\mathbf{R}_{0n}\).

La résolution inverse est indéterminée quand \(\theta = 0\) ou \(\pi\). En dehors de cette singularité de représentation, les angles peuvent être obtenus à l’aide de la fonction \(\text{atan2}\) :

• Pour \(r_{33} \neq \pm 1 \, (\theta \neq 0 \text{et } \theta \neq \pi)\), à l’aide des termes \(_{13}\) et \(_{23}\) de l’équation (3) il est possible de déterminer l’angle \(\phi\) car \(\theta \in \left[0, 180^{\circ} \right]\) (son sinus est donc positif), d’où :

  \[ \begin{equation} \phi = \text{atan2}(r_{13},-r_{23}) \end{equation} \]

  De même, à partir des termes \(_{31}\) et \(_{32}\) on obtient :

  \[ \begin{equation} \psi = \text{atan2}(r_{31},r_{32}) \end{equation} \]

  Et enfin, des termes \(_{31}\), \(_{32}\) et \(_{33}\) on peut écrire :

  \[ \begin{equation} \theta = \text{atan2}(\sqrt{r_{31}^2+r_{32}^2},r_{33}) \end{equation} \]

• Pour \(r_{33} = 1\) \((\theta = 0)\), alors :

  \[ \begin{equation} \phi + \psi = \text{atan2}(r_{21},r_{11}) \end{equation} \]

• Pour \(r_{33} = -1\) \((\theta = \pi)\), alors :

  \[ \begin{equation} \phi - \psi = \text{atan2}(r_{21},r_{11}) \end{equation} \]

Dans les deux derniers cas, \(\phi\) et \(\psi\) et restent indéterminés.

Remarque

Il est important de noter que cette succession de transformations \(\text{rot} \left(\overrightarrow{z_0}, \phi \right)\), \(\text{rot} \left(\overrightarrow{x_i}, \theta \right)\), \(\text{rot} \left(\overrightarrow{z_{ii}}, \psi \right)\) correspond à la notation originale des angles d’Euler. Cependant, il est possible de trouver des variantes de cette succession de rotations sous différents formats, amenant donc à différentes solutions. Le principe des angles d’Euler est d’utiliser le même axe de rotation pour les première et troisième transformations. Les deuxième et troisième rotations sont autour d’axes issus de la rotation précédente. Elles sont donc qualifiées d”intrinsèques. Ainsi, six combinaisons sont possibles :

1. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{x_i}\right)\), \(\text{rot} \left(\overrightarrow{z_{ii}}\right)\)

2. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_i}\right)\), \(\text{rot} \left(\overrightarrow{x_{ii}}\right)\)

3. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_i}\right)\), \(\text{rot} \left(\overrightarrow{y_{ii}}\right)\)

4. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_i}\right)\), \(\text{rot} \left(\overrightarrow{z_{ii}}\right)\)

5. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_i}\right)\), \(\text{rot} \left(\overrightarrow{x_{ii}}\right)\)

6. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_i}\right)\), \(\text{rot} \left(\overrightarrow{y_{ii}}\right)\)

Il est également possible de trouver ces six combinaisons de trois rotations autours d’axes fixes, de la base de départ. Les rotations seront alors qualifiées d”extrinsèques.

1. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\)

2. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\)

3. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\)

4. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\)

5. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\)

6. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\)

Angles de Tait - Bryan : roulis-tangage-lacet

La seule différence avec les angles d’Euler est qu’il s’agit de trois rotations consécutives autour d’axes différents :

• une rotation autour de \(\overrightarrow{z_0} \), d’angle \(\phi\) (angle de Roulis) ;

• une rotation autour de \(\overrightarrow{y_i} \), d’angle \(\theta\) (angle de Tangage) ;

• une rotation autour de \(\overrightarrow{x_{ii}} \), d’angle \(\psi\) (angle de Lacet).

Ces trois rotations sont aussi nommées « RTL ». L’appellation anglaise de ces rotations successives est « roll, pitch, yaw ». Ce paramétrage est particulièrement utilisé dans l’aéronautique (Fig. 9).

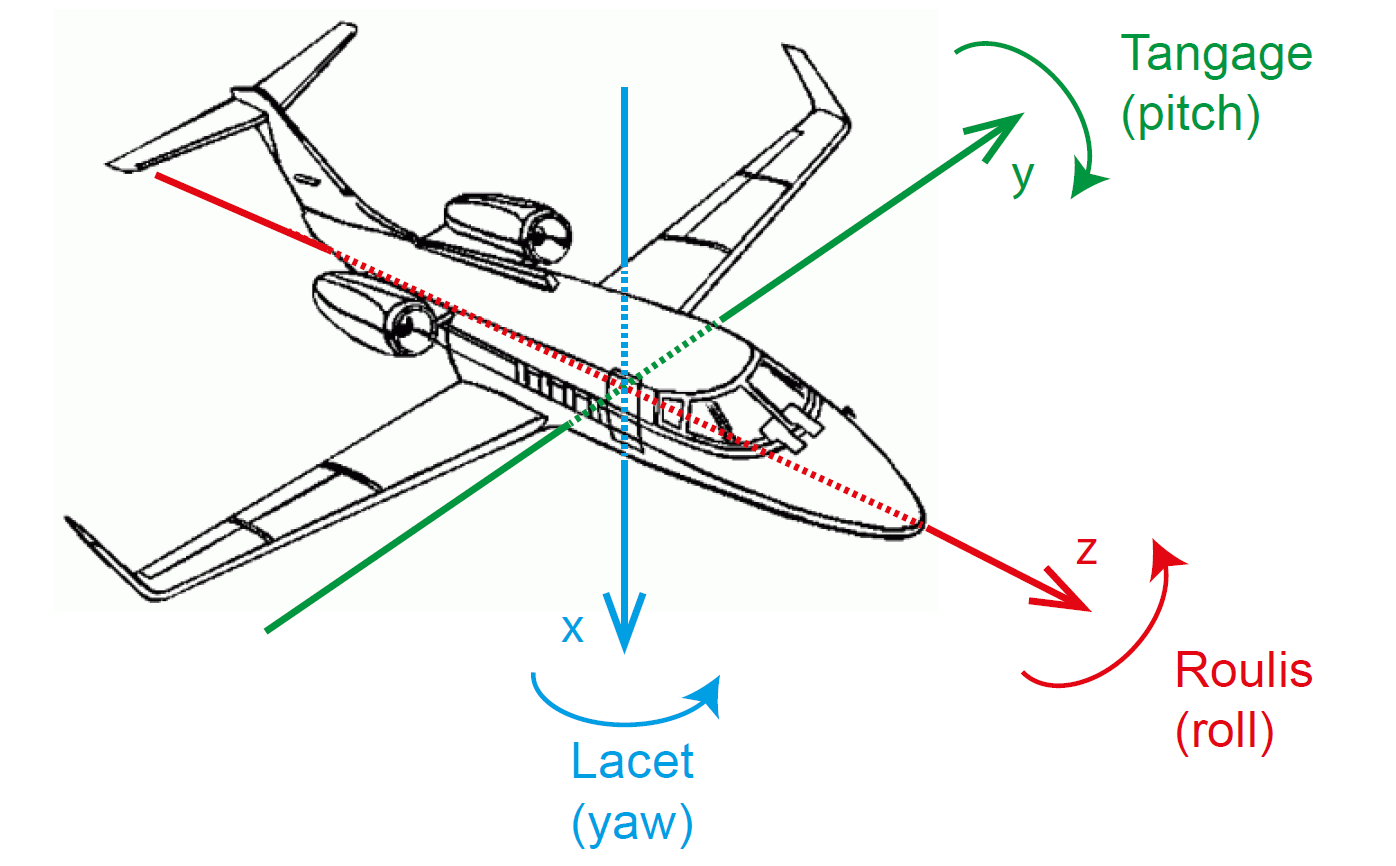
Fig. 9 Visualisation des angles de Roulis, Tangage, Lacet, en aéronautique

Lorsque ces rotations sont intrinsèques (basées sur les repères construits à chaque étape), ce paramétrage aboutit à la matrice globale suivante :

\[\begin{split} \begin{equation} \mathbf{R}_{0n} = \begin{bmatrix} \text{C}\phi & -\text{S}\phi & 0 \\ \text{S}\phi & \text{C}\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \text{C}\theta & 0 & \text{S}\theta \\ 0 & 1 & 0 \\ -\text{S}\theta & 0 & \text{C}\theta \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \text{C}\psi & -\text{S}\psi \\ 0 & \text{S}\psi & \text{C}\psi \end{bmatrix} \end{equation} \end{split}\]

(4)\[\begin{split} \begin{equation} \Leftrightarrow \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} = \begin{bmatrix} \text{C}\phi \text{C}\theta & \text{C}\phi\text{S}\theta\text{S}\psi - \text{S}\phi\text{C}\psi & \text{C}\phi\text{S}\theta\text{C}\psi + \text{S}\phi\text{S}\psi\\ \text{S}\phi\text{C}\theta & \text{S}\phi\text{S}\theta\text{S}\psi + \text{C}\phi\text{C}\psi & \text{S}\phi\text{S}\theta\text{S}\psi-\text{C}\phi\text{S}\psi\\ \text{S}\theta & \text{C}\theta\text{S}\psi & \text{C}\theta \text{C}\psi \end{bmatrix} \end{equation} \end{split}\]

Résolution inverse

Ce paramétrage présente également une singularité de représentation pour \(\theta = \pm \frac{\pi}{2}\), où la valeur de \(\psi\) est indéterminée.

• Pour \(r_{11} \neq 0 \, (\theta \text{et } \phi \neq \pi/2)\), et \(r_{33} \neq 0 \, (\theta \text{et } \psi \neq \pi/2)\), à l’aide des termes \(_{11}\) et \(_{21}\) de l’équation (4) il est possible de déterminer l’angle \(\theta\) :

  \[ \begin{equation} \phi = \text{atan2}(r_{21},r_{11}) \end{equation} \]

  De même, à partir des termes \(_{31}\), \(_{32}\) et \(_{33}\) on obtient :

  \[ \begin{equation} \theta = \text{atan2}(-r_{31},\sqrt{r_{32}^2+r_{33}^2}) \end{equation} \]

  Et enfin,

  \[ \begin{equation} \psi = \text{atan2}(r_{32},r_{33}) \end{equation} \]

• Pour \(r_{11} = 0 \, (\theta = \pm \frac{\pi}{2})\), on exploite les termes \(_{31}\), \(_{23}\) et \(_{22}\) :

  \[ \begin{equation} \theta = -r_{31} \frac{\pi}{2} \end{equation} \]
  \[ \begin{equation} \psi =\, \text{valeur arbitraire} \end{equation} \]
  \[ \begin{equation} \phi = \text{atan2}(-r_{31} r_{23},r_{22})-r_{31} \psi \end{equation} \]

Remarque

Comme avec les angles d’Euler, il existe six combinaisons possibles pour le paramétrage des angles de Tait Bryan avec des rotations intrinsèques :

1. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_i}\right)\), \(\text{rot} \left(\overrightarrow{z_{ii}}\right)\)

2. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_i}\right)\), \(\text{rot} \left(\overrightarrow{x_{ii}}\right)\)

3. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{x_i}\right)\), \(\text{rot} \left(\overrightarrow{y_{ii}}\right)\)

4. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_i}\right)\), \(\text{rot} \left(\overrightarrow{y_{ii}}\right)\)

5. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_i}\right)\), \(\text{rot} \left(\overrightarrow{z_{ii}}\right)\)

6. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_i}\right)\), \(\text{rot} \left(\overrightarrow{x_{ii}}\right)\)

Voici les six combinaisons de trois rotations extrinsèques pour le paramétrage de Tait Bryan.

1. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\)

2. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\)

3. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\)

4. \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\)

5. \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\)

6. \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\)

Relations entre rotations extrinsèques et rotations intrinsèques

A chaque rotation extrinsèque, il est possible de formuler une transformation équivalente sous forme intrinsèque. Pour cela, il faut inverser les rotations successives tout en conservant les mêmes angles.

\[\begin{split} \begin{align} \mathbf{R}_{0n} &= \mathbf{R}_{01}\left(\overrightarrow{z_0},\phi \right) \mathbf{R}_{12}\left(\overrightarrow{y_i},\theta \right) \mathbf{R}_{2n}\left(\overrightarrow{x_{ii}},\psi \right) \\ &= \mathbf{R}_{01}\left(\overrightarrow{x_0},\psi \right) \mathbf{R}_{12}\left(\overrightarrow{y_0},\theta \right) \mathbf{R}_{2n}\left(\overrightarrow{z_0},\phi \right) \\ \end{align} \end{split}\]

Exemple

La Fig. 10 avec le paramétrage d’Euler (équation (5)), la transformation intrinsèque :

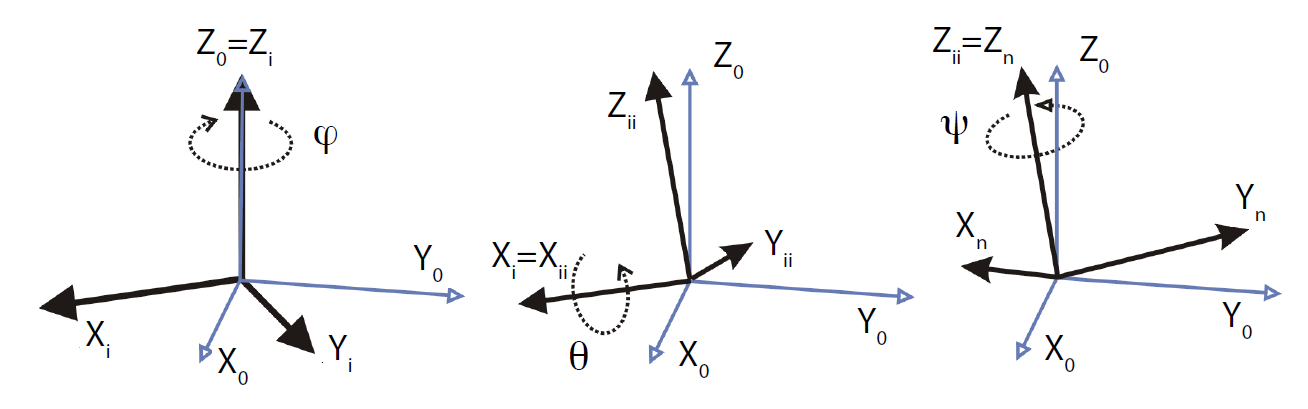
Fig. 10 Rotations dans les bases successives : Euler intrinsèque \(-60^{\circ}\), \(30^{\circ}\), \(45^{\circ}\)

(5)\[ \begin{equation} \mathbf{R}_{0n} = \mathbf{R}_{01}\left(\overrightarrow{z_0},\phi = - 60^{\circ} \right) \mathbf{R}_{12}\left(\overrightarrow{x_1},\theta = 30^{\circ}\right) \mathbf{R}_{2n}\left(\overrightarrow{z_2},\psi=45^{\circ} \right) \end{equation} \]

est équivalente à la transformation extrinsèque suivante (Fig. 11 et équation (6)) :

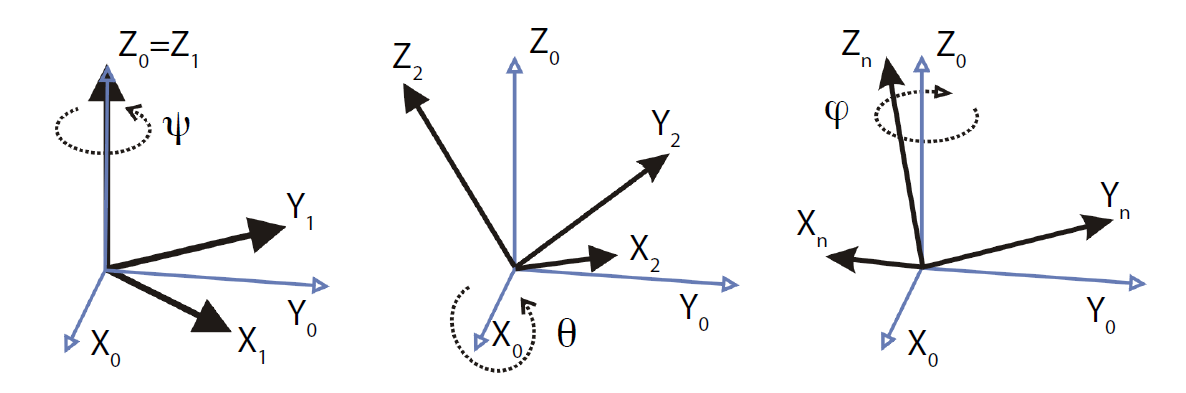
Fig. 11 Rotations autour d’axes de la base fixe : Euler extrinsèque \(45^{\circ}\), \(30^{\circ}\), \(-60^{\circ}\)

(6)\[ \begin{equation} \mathbf{R}_{0n} = \mathbf{R}_{01}\left(\overrightarrow{z_0},\psi = 45^{\circ} \right) \mathbf{R}_{12}\left(\overrightarrow{x_0},\theta = 30^{\circ}\right) \mathbf{R}_{2n}\left(\overrightarrow{z_0},\phi=-60^{\circ} \right) \end{equation} \]

Démonstration

Soit les trois rotations associées aux angles d’Euler (forme intrinsèque) :

\[\begin{split} \begin{align*} \mathcal{B}_0 \longrightarrow \mathcal{B}_i & \qquad \qquad \text{puis} & \mathcal{B}_i \longrightarrow \mathcal{B}_{ii} & \qquad \qquad \text{puis} & \mathcal{B}_{ii} \longrightarrow \mathcal{B}_{n}\\ \mathbf{R} \left(\overrightarrow{z_0}, \phi \right) & & \mathbf{R} \left(\overrightarrow{x_i}, \theta \right) & & \mathbf{R} \left(\overrightarrow{z_{ii}}, \psi \right) \end{align*} \end{split}\]

Cette succession de rotations peut être exprimée dans la base de référence \(\mathcal{B}_0\). Ainsi un point \(P_0\) se trouve modifié par la première rotation :

\[ \begin{equation} ^0 \mathbf{P}_i = \mathbf{R}\left(\overrightarrow{z_0},\phi \right)\ ^0 \mathbf{P}_0 \end{equation} \]

Il est nécessaire de changer de base le nouveau vecteur avant de faire la rotation suivante qui est définie dans la base \(\mathcal{B}_i\) :

\[ \begin{equation} ^i \mathbf{P}_{ii} = \mathbf{R}\left(\overrightarrow{x_i},\theta \right) \mathbf{R}_{i0} \mathbf{R}\left(\overrightarrow{z_0},\phi \right)\ ^0 \mathbf{P}_0 \end{equation} \]

On procède ainsi pour les rotations suivantes et on exprime le résultat dans \(\mathcal{B}_0\) en passant par la base \(\mathcal{B}_3\) :

\[ \begin{equation} ^0 \mathbf{P}_n = \mathbf{R}_{0n} \mathbf{R}_{n(ii)} \mathbf{R}\left(\overrightarrow{z_ii},\psi \right) \mathbf{R}_{(ii)i} \mathbf{R}\left(\overrightarrow{x_i},\theta \right) \mathbf{R}_{i0} \mathbf{R}\left(\overrightarrow{z_0},\phi \right)\ ^0 \mathbf{P}_0 \end{equation} \]

or

\[ \begin{equation} \mathbf{R}\left(\overrightarrow{z_0},\phi \right) = \mathbf{R}_{0i} \quad \mathbf{R}\left(\overrightarrow{x_i},\theta \right) = \mathbf{R}_{i(ii)} \quad \mathbf{R}\left(\overrightarrow{z_{ii}},\psi \right) = \mathbf{R}_{(ii)n} \end{equation} \]

d’où

\[ \begin{equation} ^0 \mathbf{P}_n = \mathbf{R}_{0n} \mathbf{I}_3 \mathbf{I}_3 \mathbf{I}_3 \ ^0 \mathbf{P}_0 \end{equation} \]

qui peut encore se réécrire :

\[ \begin{equation} ^0 \mathbf{P}_n = \mathbf{R}_{0i} \mathbf{R}_{i(ii)} \mathbf{R}_{(ii)n} \ ^0 \mathbf{P}_0 \end{equation} \]

or

\[ \begin{equation} \mathbf{R}_{0i} = \mathbf{R}\left(\overrightarrow{z_0},\phi \right) \quad \mathbf{R}_{i(ii)} = \mathbf{R}\left(\overrightarrow{x_0},\theta \right) \quad \mathbf{R}_{(ii)n} = \mathbf{R}\left(\overrightarrow{z_0},\psi \right) \end{equation} \]

d’où :

\[ \begin{equation} ^0 \mathbf{P}_n = \mathbf{R}\left(\overrightarrow{z_0},\phi \right) \mathbf{R}\left(\overrightarrow{x_0},\theta \right) \mathbf{R}\left(\overrightarrow{z_0},\psi \right) \ ^0 \mathbf{P}_0 \end{equation} \]

ce qui correspond aux rotations dans la base fixe \(\mathcal{B}_0\) (forme extrinsèque) :

\[\begin{split} \begin{align*} \mathcal{B}_0 \longrightarrow \mathcal{B}_{0+\psi} & \qquad \qquad \text{puis} & \mathcal{B}_0 \longrightarrow \mathcal{B}_{0+\theta} & \qquad \qquad \text{puis} & \mathcal{B}_{0} \longrightarrow \mathcal{B}_{0+\phi}\\ \mathbf{R} \left(\overrightarrow{z_0}, \psi \right) & & \mathbf{R} \left(\overrightarrow{x_0}, \theta \right) & & \mathbf{R} \left(\overrightarrow{z_0}, \phi \right) \end{align*} \end{split}\]

Les quaternions

Les quaternions sont aussi appelés paramètres d’Euler ou d’Olinde Rodrigues. Dans cette représentation, l’orientation est exprimée à l’aide de quatre paramètres qui décrivent une rotation unique équivalente, d’angle \(\theta \in \left[ 0, 180^{\circ} \right]\) autour d’un axe de vecteur unitaire \(\mathbf{u}\). Les quaternions sont définis par :

\[\begin{split} \begin{equation} \begin{cases} Q_1 &= \text{C} \theta /2 \\ Q_2 &= u_x \text{S} \theta /2 \\ Q_3 &= u_y \text{S} \theta /2 \\ Q_4 &= u_z \text{S} \theta /2 \end{cases} \end{equation} \end{split}\]

Une des propriétés des quaternions est de vérifier la relation :

(7)\[ \begin{equation} Q_1^2 + Q_2^2 + Q_3^2 + Q_4^2 =1 \end{equation} \]

La matrice de rotation \(\mathbf{R}_{0n}\) pour passer de \(\mathcal{B}_0\) à \(\mathcal{B}_n\) s’écrit :

(8)\[\begin{split} \begin{equation} \mathbf{R}_{0n} = \begin{bmatrix} 2(Q_1^2+Q_2^2)-1 & 2(Q_2 Q_3 - Q_1 Q_4) & 2(Q_2 Q_4 + Q_1 Q_3) \\ 2(Q_2 Q_3 + Q_1 Q_4) & 2(Q_1^2+Q_3^2)-1 & 2(Q_3 Q_4 - Q_1 Q_2) \\ 2(Q_2 Q_4 - Q_1 Q_3) & 2(Q_3 Q_4 + Q_1 Q_2) & 2(Q_1^2+Q_4^2)-1 \\ \end{bmatrix} \end{equation} \end{split}\]

Résolution inverse

En identifiant terme à terme les coefficients de la matrice précédente avec :

\[\begin{split} \begin{equation} \mathbf{R}_{0n} = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{bmatrix} \end{equation} \end{split}\]

il est possible d’exprimer chacun des quaternions :

\[\begin{split} \begin{equation} \begin{cases} Q_1 = 1/2 \sqrt{1+r_{11}+r_{22}+r_{33}} \\ Q_2 = 1/2 \text{sgn}(r_{32}-r_{23})\sqrt{1+r_{11}-r_{22}-r_{33}} \\ Q_3 = 1/2 \text{sgn}(r_{13}-r_{31})\sqrt{1-r_{11}+r_{22}-r_{33}} \\ Q_4 = 1/2 \text{sgn}(r_{21}-r_{12})\sqrt{1-r_{11}-r_{22}+r_{33}} \\ \end{cases} \end{equation} \end{split}\]

Bien que l’utilisation de quatre paramètres rende ce formalisme redondant (équation (7)), il a l’avantage de ne présenter aucune représentation singulière (contrairement aux paramétrages d’Euler et Bryan).

Solutions industrielles

Diverses conventions sont utilisées dans les modeleurs géométriques et le contrôleurs de robot. Voici quelques exemples :

• Adept et Stäbli : \(\text{rot} \left( \overrightarrow{z_0} \right)\), \(\text{rot} \left(\overrightarrow{y_i} \right)\), \(\text{rot} \left(\overrightarrow{z_{ii}}\right)\)

• Bosch : \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\)

• Fanuc et Kuka : \(\text{rot} \left(\overrightarrow{x_0}\right)\), \(\text{rot} \left(\overrightarrow{y_0}\right)\), \(\text{rot} \left(\overrightarrow{z_0}\right)\)

• ABB : \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot} \left(\overrightarrow{y_i}\right)\), \(\text{rot} \left(\overrightarrow{x_{ii}}\right)\) ainsi que les quaternions

• CATIA et Solidworks : \(\text{rot} \left(\overrightarrow{z_0}\right)\), \(\text{rot}\left(\overrightarrow{x_i}\right)\), \(\text{rot}\left(\overrightarrow{z_{ii}}\right)\)