TD n°2 : MGI par la méthode de Paul, singularités

On étudie le robot 6 axes RX90 de marque Stäubli donné en Fig. 33 :

Fig. 33 Robot STAUBLI RX90

L’objectif du TD est de calculer l’ensemble des solutions au Modèle Géométrique Inverse (MGI) pour ce type de robot en utilisant la méthode de Paul. L’analyse de la résolution et des équations mises en jeu permet de déterminer les singularités du robot.

Analyse du paramétrage

Le schéma cinématique du robot ainsi que le paramétrage selon la convention de Denavit et Hartenberg modifiée sont donnés en annexe.

Question 1.1 : Reporter sur le schéma cinématique les différents points caractéristiques, constantes géométriques, et paramètres articulaires.

Question 1.2 : Rappeler quelle est la particularité de cette structure permettant de découpler le problème de résolution du MGI en deux sous problèmes :

• le problème en position;

• le problème en orientation.

Résolution du Modèle géométrique Inverse

Dans cette partie, il s’agit de mettre en oeuvre la méthode de résolution dite « de Paul » pour résoudre le MGI en deux temps.

Question 2.1 : Exprimer l’équation en position : expression de l’origine de \(O_4\) dans le référentiel de base \(\mathcal{R}_0\) en fonction des matrices de transformation homogènes mises en jeu. De quels paramètres articulaires dépend la position du point \(O_4\) ?

Question 2.2 : Déterminer par la méthode de Paul l’ensemble des solutions articulaires obtenues par l’équation en position.

Question 2.3 : Exprimer l’équation en orientation : expression de la base orientant l’effecteur dans le référentiel de base \(\mathcal{B}_0\) en fonction des matrices de rotation (changement de bases) mises en jeu. Une fois le problème en position résolu, de quels paramètres articulaires dépend l’orientation de l’effecteur ?

Question 2.4 : Déterminer par la méthode de Paul l’ensemble des solutions articulaires obtenues par l’équation en orientation.

Synthèse

Question 3.1 : Faire le bilan sur le nombre de solutions articulaires correspondant à un positionnement du repère effecteur.

Question 3.2 : Importer le robot dans l’application « RoboDK », puis, sur quelques configurations, étudier les solutions (notamment leur nombre) au MGI.

Question 3.3 : À partir des équations obtenues en partie 2, déterminer et illustrer les singularités géométriques de ce robot.

Annexes

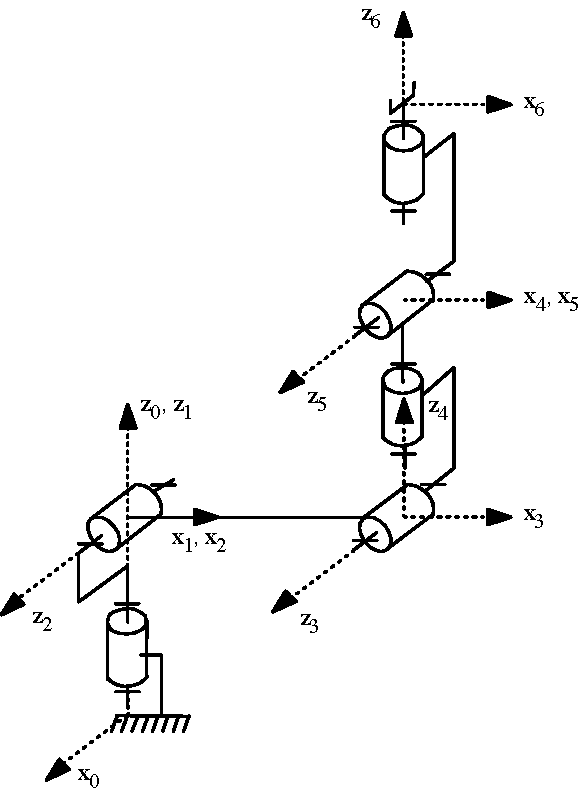
Fig. 34 Schéma cinématique

	\(d_i\)	\(\alpha_i\)	\(r_i\)	\(\theta_i\)
\(\mathbf{T}_{01}\)	0	0	\(r_1\)	\(\theta_1\)
\(\mathbf{T}_{12}\)	0	\(90^{\circ}\)	0	\(\theta_2\)
\(\mathbf{T}_{23}\)	\(d_3\)	0	0	\(\theta_3\)
\(\mathbf{T}_{34}\)	0	\(-90^{\circ}\)	\(r_4\)	\(\theta_4\)
\(\mathbf{T}_{45}\)	0	\(90^{\circ}\)	0	\(\theta_5\)
\(\mathbf{T}_{56}\)	0	\(-90^{\circ}\)	\(r_6\)	\(\theta_6\)

Matrices homogènes élémentaires de transformations entre repères :

\[\begin{split} \begin{align*} \mathbf{T}_{01}&= \begin{bmatrix} \text{C}\theta_1 & -\text{S}\theta_1 & 0 & 0 \\ \text{S}\theta_1 & \text{C}\theta_1 & 0 & 0 \\ 0 & 0 & 1 & r_{1} \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{12}&= \begin{bmatrix} \text{C}\theta_2 & -\text{S}\theta_2 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ \text{S}\theta_2 & \text{C}\theta_2 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{23}&= \begin{bmatrix} \text{C}\theta_3 & -\text{S}\theta_3 & 0 & d_3 \\ \text{S}\theta_3 & \text{C}\theta_3 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{34}&= \begin{bmatrix} \text{C}\theta_4 & -\text{S}\theta_4 & 0 & 0 \\ 0 & 0 & 1 & r_4 \\ -\text{S}\theta_4 & -\text{C}\theta_4 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{45}&= \begin{bmatrix} \text{C}\theta_5 & -\text{S}\theta_5 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ \text{S}\theta_5 & \text{C}\theta_5 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ \\ \mathbf{T}_{56}&= \begin{bmatrix} \text{C}\theta_6 & -\text{S}\theta_6 & 0 & 0 \\ 0 & 0 & 1 & r_6 \\ -\text{S}\theta_6 & -\text{C}\theta_6 & 0 & 0 \\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{align*} \end{split}\]

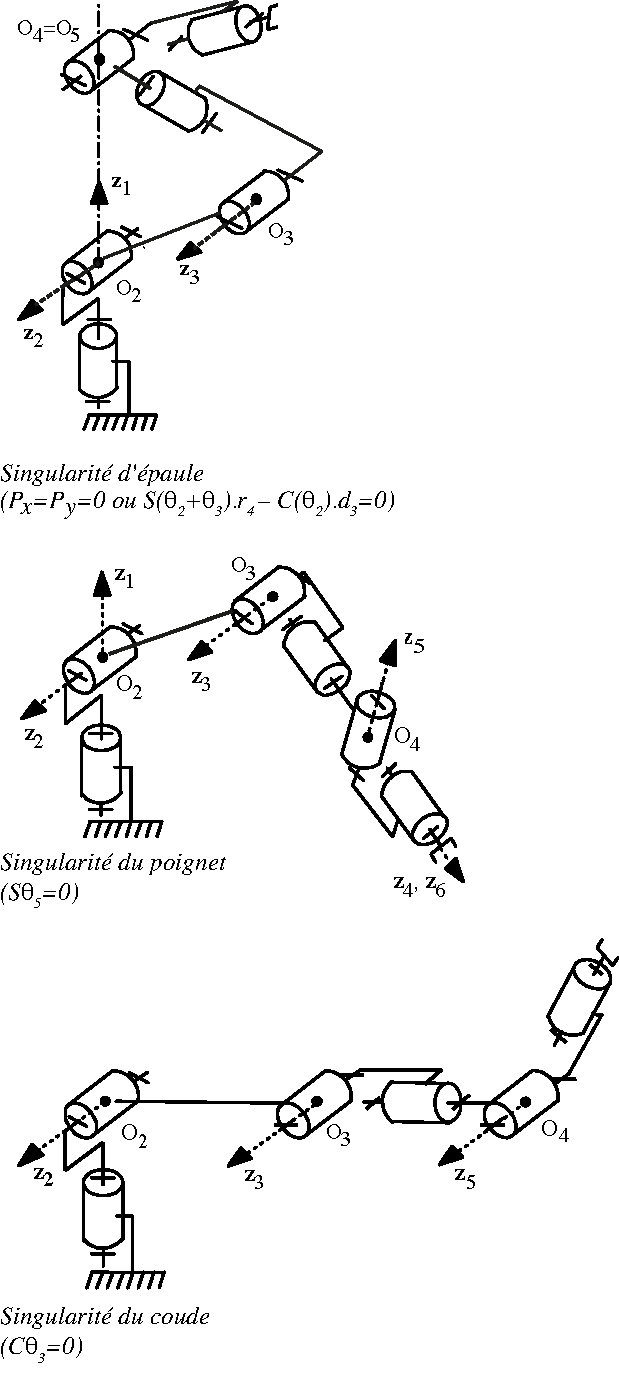
Fig. 35 Positions singulières