TP : Étude d’un robot parallèle - Spiderbot#
Le robot SpiderBot (Fig. 58) est une imprimante 3D possédant une architecture de type « delta ». L’enveloppe de travail de ce système est contenue dans un espace cylindrique de rayon \(90 mm\) et de hauteur \(200 mm\). Son architecture particulière dite « delta » permet d’obtenir des déplacements rapides et des accélérations de niveau élevé. Ce type d’architecture permet également de diminuer le coût de fabrication de la machine du fait des 3 jambes identiques.

Fig. 58 robot Spiderbot#
Découverte et prise en main du système#
L’objectif de cette partie est de découvrir le système, son fonctionnement et les quelques solutions technologiques particulières au travers de manipulation et d’analyse des documents ressources.
Question 1.1 : Effectuer la procédure de démarrage de l’imprimante 3D fournie dans les documents ressources à la fin du sujet.
Question 1.2 : Réaliser quelques déplacements manuels de faible amplitude pour repérer les différents corps et assimiler les mouvements et liaisons ; faire attention aux collisions.
Question 1.3 : Analyser la solution technologique mise en place pour réaliser la liaison entre une barre et l’ensemble tête d’impression 3D (Fig. 59).
Question 1.4 : Déterminer la stratégie retenue par le constructeur pour connaître la position de la tête d’impression dans le référentiel du plateau.
Étude des modèles géométriques inverse et direct#
Schéma cinématique#
L’objet de cette partie est de mettre en place un paramétrage sur le mécanisme permettant de repérer les positions de chaque composant en vue de la construction des modèles géométrique inverse et direct.
Question 2.1 : Proposer un modèle cinématique de l’ensemble en ne considérant qu’une seule jambe.
Question 2.2 : En utilisant les Fig. 60 et Fig. 61 proposer un paramétrage géométrique minimal de la structure.
Question 2.3 : Pour ce robot, préciser :
les variables de l’espace des tâches
le paramétrage en position est-il de type cartésien ? polaire ? sphérique ?
le paramétrage en orientation est-il de type Euler ? Bryan ? quaternions ? extrinsèque ? intrinsèque ?
les variables de l’espace articulaire
les autres paramètres considérés comme constantes géométriques
Modèle géométrique inverse#
L’objectif de cette partie est de proposer, d’implémenter et de valider un modèle géométrique inverse.
Question 2.4 : En utilisant le paramétrage défini précédemment, déterminer les équations du modèle géométrique inverse.
Question 2.5 : Implémenter le modèle géométrique inverse déterminé à la question précédente sur dans le fichier Matlab nommé ecriture_equations_MGI_symbolique.m, sur les lignes 8 à 10. Déclarer chaque paramètre en tant que variable symbolique sur la ligne 5 de ce même fichier.
Question 2.6 : Mesurer les dimensions des paramètres qui sont des constantes géométriques pour ce modèle. Saisir dans le fichier ecriture_vecteurs_parametres.m à la ligne 3 les noms des variables symboliques représentant ces constantes géométriques. Saisir ensuite, dans le même ordre, leur valeurs numériques à la ligne 5. Donner à la ligne 8 l’index du paramètre de longueur de barre, dans le vecteur de paramètre construit précédemment (ligne 3).
Question 2.7 : Valider expérimentalement votre modèle en effectuant une mesure sur la machine à l’aide d’un réglet. Pour cela :
se déplacer à une position quelconque dans l’espace des tâches et mesurer les valeurs articulaires correspondantes
rentrer la position de l’espace des tâches dans le fichier donnees_point.m à la place des valeurs présentes
sélectionner le cas étudié nommé « point » en dé-commentant la ligne 44 du fichier Main.m et en mettant en commentaire les autres cas d’étude
comparer les positions articulaires issues des mesures expérimentales et celles issues du modèle après exécution du fichier Main.m
Modèle géométrique direct#
Question 2.8 : Proposer une démarche afin de calculer le modèle géométrique direct.
Question 2.9 : Analyser qualitativement la solution retenue dans le fichier definition_fonction_TGD.m pour résoudre le modèle géométrique direct.
Étude de l’influence d’un défaut géométrique sur le comportement du système#
L’objectif de cette partie est de prédire la géométrie d’une pièce produite via l’imprimante 3D en considérant que les paramètres géométriques de celle-ci sont mal connus. Pour ce faire, nous allons modifier un paramètre géométrique (la longueur des barres) et nous analyserons ensuite les résultats issus de la simulation et de la mesure de la pièce réalisée.
Impression d’une pièce avec défauts (1h30 avant la fin du TP)#
Avec l’aide du professeur exécuter la procédure suivante pour modifier les paramètres de la machine :
démarrer le logiciel Repetier.host
connecter l’imprimante 3D et attendre quelques secondes que la connexion s’établisse
en utilisant l’outil eeprom depuis le menu, modifier les paramètres suivants :
diagonal rod length (initialement \(255.55 mm\)) devient \(245.55 mm\)
Z max length (initialement \(251.205 mm\)) devient \(251.700 mm\)
Question 3.1 : Expliquer ce qui a été réalisé et pourquoi deux paramètres ont été modifiés.
Analyse de l’influence d’un défaut#
Question 3.2 : Modifier le fichier ecriture_vecteurs_parametres.m, ligne 5 pour saisir la « valeur vraie » de longueur de barre; le défaut d’identification de cette valeur est saisi sur la ligne 7.
Question 3.3 : Exécuter le fichier Main.m pour les deux cas d’étude pré-programmés, nommés « grille » et « cercle » en les dé-commentant / commentant successivement (lignes 44 à 46). Analyser les affichages réalisés dans la fenêtre de commande Matlab ainsi qu’au travers des différentes figures.
Question 3.4 : Mesurer le défaut dimensionnel sur la pièce et le comparer par rapport à la simulation issue du modèle. Comparer également le défaut de circularité donné par mesure sur le Talyrond (Fig. 62 et Fig. 63) à la simulation de ce défaut.
S’il vous reste du temps#
Question 3.5 : Calculer de manière analytique l’écart entre deux points diamétralement opposés du cercle précédent tracé.
Question 3.6 : Simuler l’effet d’un autre défaut et analyser la cartographie d’erreur.
Documents ressources#
Les pages suivantes regroupent un certain nombre de documents permettant d’appréhender le fonctionnement du système ainsi que ses composants technologiques.
Notice d’allumage/arrêt du robot Spiderbot + Notice de changement des paramètres eeprom

Fig. 59 Liaison entre les barres et la tête d’impression#
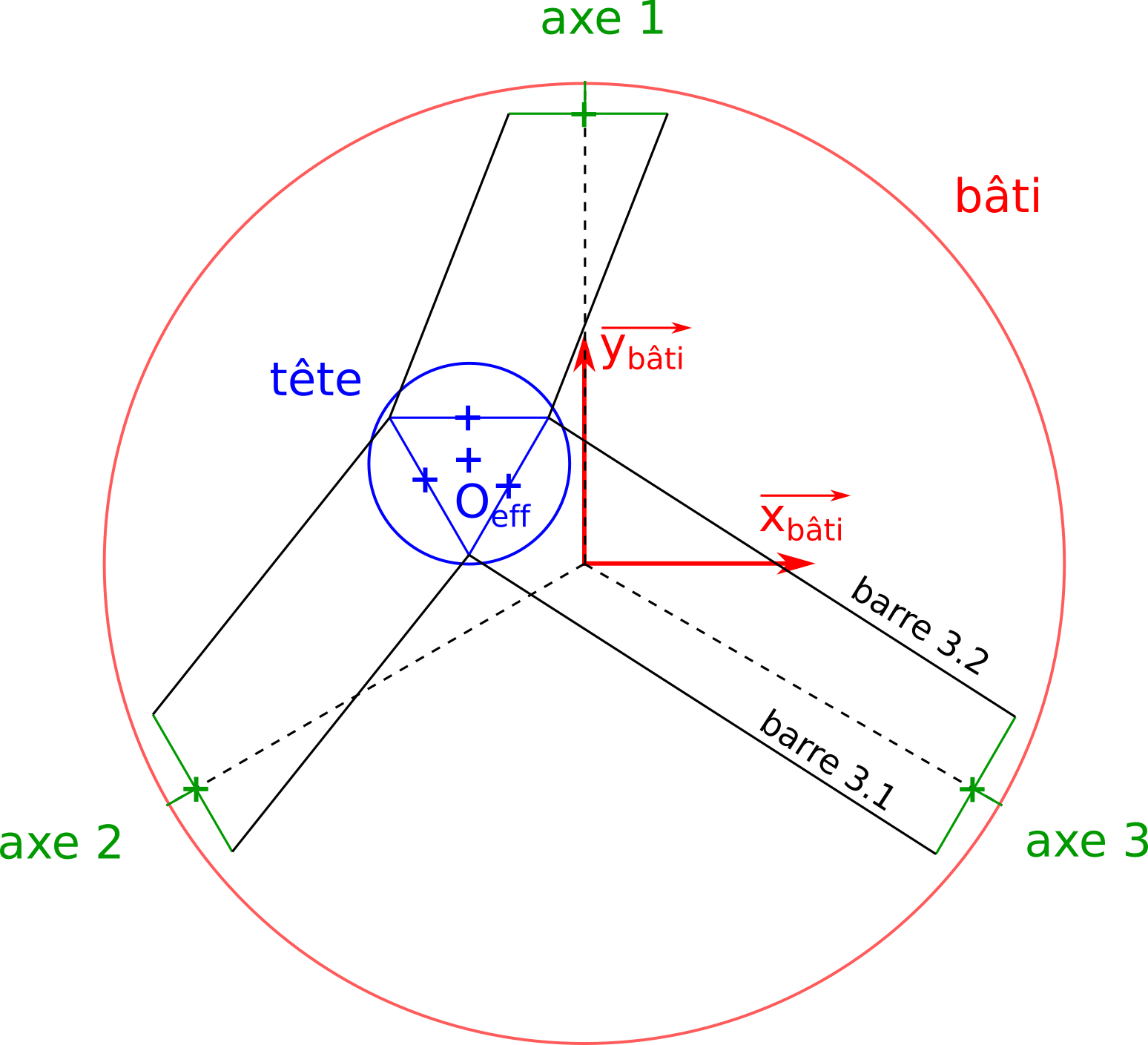
Fig. 60 Schéma de l’architecture de l’imprimante vue de dessus#
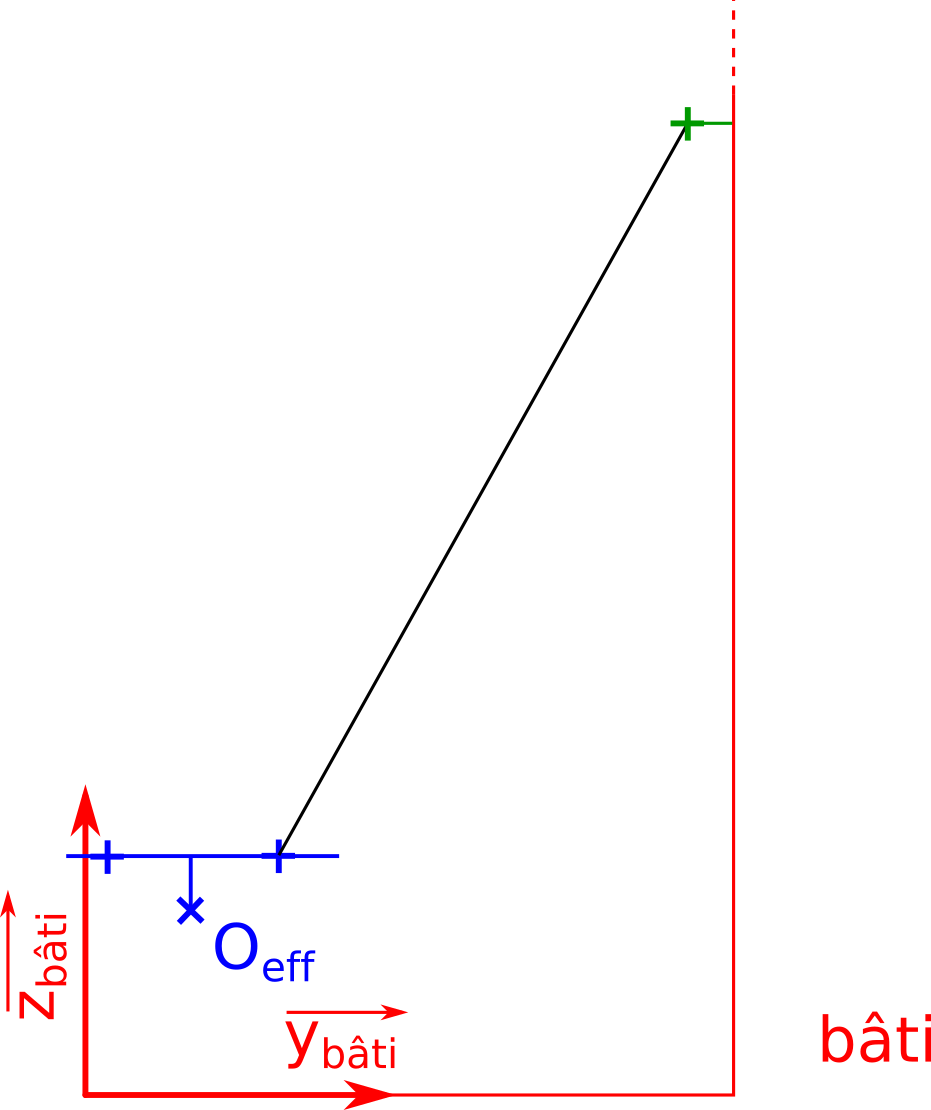
Fig. 61 Schéma de l’architecture de l’imprimante vue dans un plan latéral#

Fig. 62 Photo de mesure de circularité au Talyrond#
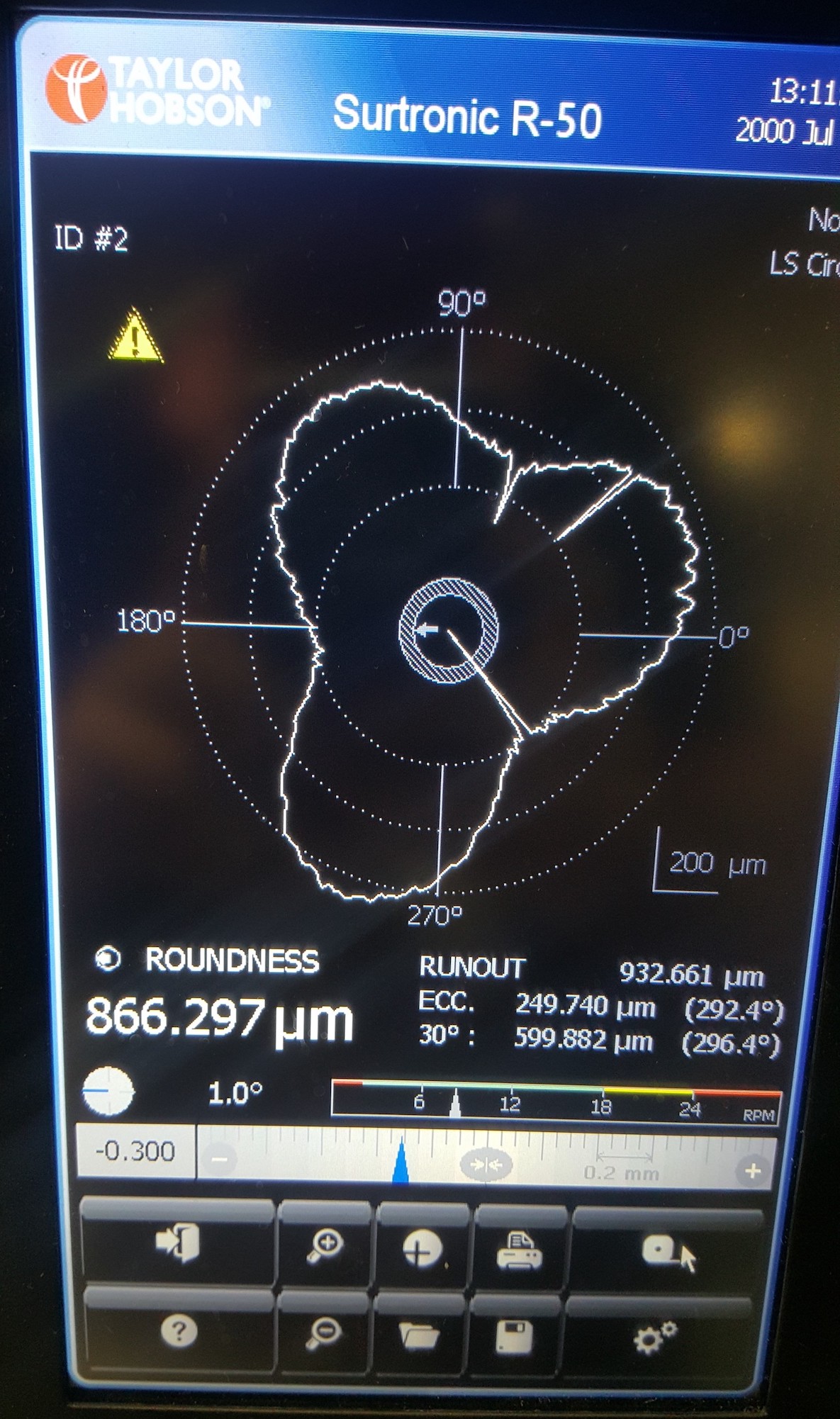
Fig. 63 Zoom sur le résultat de circularité#
