Algorithme de Newton-Raphson

La méthode de Newton, aussi appelée méthode de Newton-Raphson est un algorithme de recherche de racine d’une fonction \(f(x)\), au voisinage d’une racine supposée. La méthode proposée par Isaac Newton fut publiée en 1685 ; elle était alors uniquement appliquée aux polynômes, ne calculait pas les approximations successives \(x_n\) et aboutissait directement à une approximation de la racine recherchée, par une séquence compliquée de polynômes. En 1690, Joseph Raphson publia une version simplifiée, décrivant la méthode en terme d’approximations successives, mais considéra encore cette méthode purement algébrique et réduite aux polynômes.

Elle est basée sur l’expression de la fonction \(f(x)\) sous forme de série de Taylor en \(x_0\) (\(f\) est supposée indéfiniment dérivable) :

\[\begin{split} \begin{align} f(x) &= f(x_0) + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^{2} + \frac{f^{(3)}(x_0)}{3!}(x-x_0)^{3} + \cdots\\ &= \sum^{\infty}_{n=0} \frac{f^{(n)}(x_0)}{n!}(x-x_0)^{n} \end{align} \end{split}\]

où \(n!\) est la factorielle de \(n\) et \(f^{(n)}(x_0)\) désigne la dérivée n-ième de \(f\) au point \(x_0\). Appliquée au point \(x = x_0 + \epsilon\), l’expression de la série de Taylor est :

\[ \begin{equation} f(x_0+\epsilon) = f(x_0) + f'(x_0)\epsilon + \frac{1}{2} f''(x_0) \epsilon^2 + \cdots \end{equation} \]

En ne conservant que le terme du premier ordre, on obtient :

(23)\[ \begin{equation} f(x_0+\epsilon) \approx f(x_0) + f'(x_0)\epsilon \end{equation} \]

Cette équation(23) est l’équation de la droite tangente à la courbe au point \((x_0, f(x_0))\). Le point \((x_1, 0)\) est à l’intersection entre la droite tangente et l’axe des abscisses (Fig. 22). Cette expression permet d’estimer le déplacement à effectuer \(\epsilon\) à partir du point initial \(x_0\) pour se rapprocher de la racine. En effet, en posant :

\[ \begin{equation} f(x_0+\epsilon) = 0 \end{equation} \]

et en résolvant l’équation (X), au premier pas d’itération \((\epsilon = \epsilon_0 )\) on trouve :

\[ \begin{equation} \epsilon_0 = - \frac{f(x_0)}{f'(x_0)} \end{equation} \]

ce qui permet d’obtenir la première position estimée pour la racine :

\[ \begin{equation} x_1 = x_0 + \epsilon_0 \end{equation} \]

Ce processus peut être répété jusqu’à convergence avec une précision souhaitée en utilisant l’expression :

\[ \begin{equation} \epsilon_n = - \frac{f(x_n)}{f'(x_n)} \end{equation} \]

et donc permet d’arriver une estimation de la position de la racine :

\[ \begin{equation} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \quad \text{avec} \quad n= 1, 2, 3 \cdots \end{equation} \]

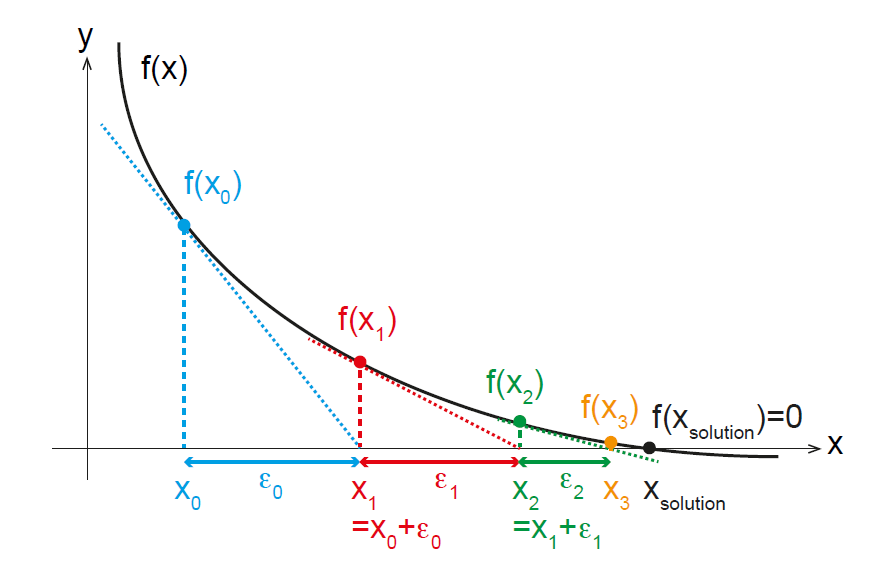
Fig. 22 Principe de convergence de la méthode de Newton-Raphson